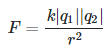कूलॉम के नियम का सदिश निरूपण vector representation of coulomb’s law in hindi, कूलाम नियम का सदिश रूप
(vector representation of coulomb’s law form in hindi) कूलॉम के नियम का सदिश निरूपण : कूलॉम के नियम के अनुसार दो बिंदु आवेश q1 & q2 के मध्य लगने वाला विद्युत बल दोनों के परिमाण (मान) के गुणनफल के समानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
ठीक इसी प्रकार
आवेश q1 से q2 की ओर वेक्टर को निम्न प्रकार लिखा जा सकता है।
ठीक इसी प्रकार आवेश q2 से q1 की ओर वेक्टर को निम्न प्रकार लिखा जा सकता है।
एकांक वेक्टर के रूप में लिखने पर दोनों को निम्न प्रकार व्यक्त किया जाता है
माना q2 से q1 आवेश पर आरोपित बल F12 vector है तथा आवेश q1 से q2 पर आरोपित बल F21 vector है तो
चूँकि हम जानते है की r12 = r21 = r
अतः
सदिश रूप में कूलाम का नियम (Coulomb’s law in vector form in hindi) : कूलाम के नियम के अनुसार दो बिंदु आवेशों q1 व q2 के बीच लगने वाला वैद्युत बल आवेशों के गुणनफल के अनुक्रमानुपाती तथा उनके मध्य की दूरी के वर्ग के व्युत्क्रमानुपाती होता है अर्थात यहाँ पर आवेशो के परिमाण |q1| एवं |q2| का प्रयोग किया गया है क्योंकि आवेश ऋणात्मक और धनात्मक कुछ भी हो सकते है एवं उसके अनुसार बल भी आकर्षण या प्रतिकर्षण प्रकृति का हो सकता है।
अत: F = K|q1||q2|/r2
यहाँ K , स्थिर वैद्युत बल नियतांक है।
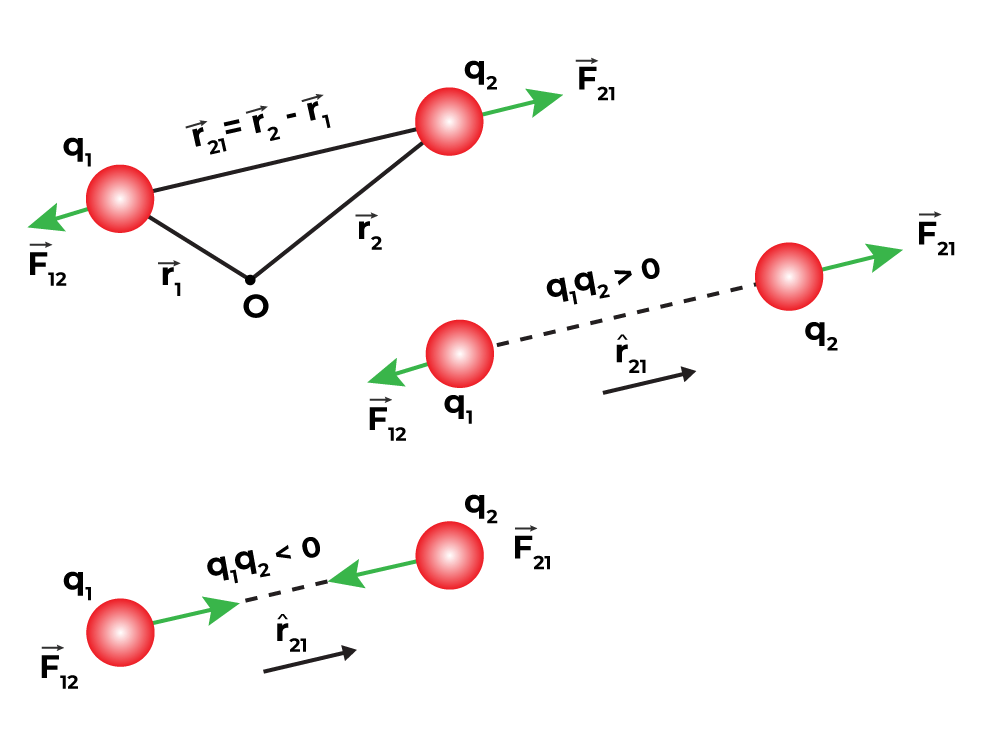
चूँकि बल सदिश राशि है अत: कुलाम बल को सदिश रूप में लिखना बेहतर होगा। माना समान प्रकृति के दो आवेश q1 व q2 बिदुओं A व B पर रखे है। ये दोनों आवेश एक दुसरे पर प्रतिकर्षण बल आरोपित करेंगे।
बिंदु A का स्थिति वेक्टर r1 = OA
बिंदु B का स्थिति वेक्टर r2 = OB
इसलिए q1 व q2 की ओर अर्थात A से B की ओर वेक्टर –
AB = r12 = r2 – r2
इसी प्रकार BA = r21 = r1 – r2
r12 का परिमाण r12 एवं r21 का परिमाण |r21| होगा।
क्योंकि किसी वेक्टर की दिशा एकांक वेक्टर द्वारा निर्धारित होती है , जिसकी दिशा उसी वेक्टर के अनुदिश होती है अत:
एकांक वेक्टर r12 = r12/ |r12|
एकांक वेक्टर r21 = r21/ |r21|
अथवा
एकांक वेक्टर r12 = r12/ |r12|
एकांक वेक्टर r21 = r21/ |r21|
हम जानते है कि एकांक सदिश = स्थिति सदिश/सदिश का परिमाण
परिमाण को सदैव || मोड़ में लिखते है।
यदि q1 व q2 पर बल F12 हो और q1 व q2 पर बल F21 हो तो –
F12 = q1q2 r21/4πE0|r21|2
और
F21 = q1q2 r12/4πE0|r12|2
और
F21 = q1q2 r12/4πE0|r12|2 समीकरण-2
समीकरण-1 और समीकरण-2 कुलाम के नियम को सदिश रूप में व्यक्त करते है।
चूँकि r21 = -r12
F12 = -F21
इसी प्रकार यदि q1 व q2 विपरीत प्रकृति के आवेश है तो वे एक दुसरे को आकर्षित करेंगे।
इस दशा में कुलाम बल –
F12 = q1q2.r12/4πE0.r122
और
F21 = q1q2.r21/4πE0.r212
r21 का स्थिति सदिश = r1 – r2
r21 का परिमाण = |r1 – r2|
यदि कोई वेक्टर निम्न प्रकार लिखा है –
r = xi + yj + zk
अत: |r| = √(i का गुणांक)2 + (j का गुणांक)2 + (k का गुणांक)2
|r| = √(x2 + y2 + z2)
answer by Lucky sir –

F21 = q2 पर q1 के कारण बल F21 = q1q2.r21/4πE0.r212
F12 = q1 पर q2 के कारण बल F12 = q1q2.r12/4πE0.r122
F12 = -F21
इसी तरह r12 = -r21
या F12 + F21 = 0
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics