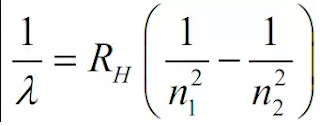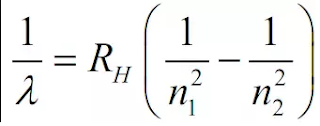क्वांटीकरण का स्पेक्ट्रमी परिमाण / बोर सिद्धांत द्वारा हाइड्रोजन परमाणु के रेखीय स्पेक्ट्रम की व्याख्या करना
2. उत्तेजित अवस्था : सामान्य अवस्था को छोड़कर परमाणु की उच्च ऊर्जा अवस्था को उत्तेजित अवस्था कहते है।
3. उत्तेजन विभव / उत्तेजन ऊर्जा : सामान्य अवस्था से इलेक्ट्रॉन को किसी विशेष उत्तेजित अवस्था में पहुँचाने के लिए आवश्यक ऊर्जा को उत्तेजन विभव या उत्तेजन उर्जा कहते है।
4. आयनन विभव / आयनन ऊर्जा / आयनन एन्थैल्पी : किसी गैसीय उदासीन परमाणु के बाह्यतम कोश से इलेक्ट्रॉन को बाहर निकालने के लिए दी गयी आवश्यक ऊर्जा को आयनन एन्थैल्पी कहते है।
5. पृथक्करण ऊर्जा : किसी विशेष उत्तेजित अवस्था से इलेक्ट्रॉन को पूर्ण रूप से बाहर निकालने के लिए दी गयी ऊर्जा को पृथक्करण ऊर्जा कहते है।
क्वांटीकरण का स्पेक्ट्रमी परिमाण / बोर सिद्धांत द्वारा हाइड्रोजन परमाणु के रेखीय स्पेक्ट्रम की व्याख्या करना
h2
h2
– 1/n22 ]
श्रेणियाँ
- लाइमन श्रेणी = पैराबैंगनी क्षेत्र।
- बामर श्रेणी = दृश्य क्षेत्र।
- पाश्चन , ब्रेकट और फुण्ड श्रेणी = अवरक्त क्षेत्र।
- हम्फ्री श्रेणी = दूर अवरक्त क्षेत्र।
बोर सिद्धांत की कमियां
- इस सिद्धान्त की सहायता से एक इलेक्ट्रॉन वाले परमाणु या आयन के रेखीय स्पेक्ट्रम की व्याख्या की जा सकती है लेकिन जिन परमाणु या आयन में एक से अधिक इलेक्ट्रॉन होते है उनके रेखीय स्पेक्ट्रम की व्याख्या नहीं की जा सकती है।
- अच्छे स्पेक्ट्रमीदर्शी द्वारा रेखीय स्पेक्ट्रम को देखने पर यह पाया गया कि यह एक रेखा नहीं है बल्कि रेखाओं का समूह है।
- विद्युत क्षेत्र की उपस्थिति में यह रेखीय पुन: कई लाइन में विभक्त हो जाता है इसे स्पेक्ट्रम स्टार्क प्रभाव कहते है , इसकी व्याख्या बोर नहीं कर सके।
- चुम्बकीय क्षेत्र की उपस्थिति में यह रेखीय स्पेक्ट्रम कई लाइन में विभक्त हो जाते है इसे जिमोन प्रभाव कहते है , बोर सिद्धांत के द्वारा इसकी व्याख्या भी नहीं की जा सकती है।
tags in english : spectrum series explanation with bohr’s model ?
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics