FOURIER SERIES OF SAWTOOTH WAVE in hindi आरादंती तरंग की फूरिये श्रेणी क्या है चित्र सहित

आरादंती तरंग की फूरिये श्रेणी क्या है चित्र सहित FOURIER SERIES OF SAWTOOTH WAVE in hindi ?

वर्गाकार तरंग की फूरिये श्रेणी ( FOURIER SERIES OF A SQUARE WAVE) जैसा चित्र (3.3-1) में दर्शाया गया है कि एक वर्गाकार तरंग x – दिशा में गति कर रही है जिसका आवर्त काल तथा विस्थापन अर्ध समय अंतराल – T/2 से 0 तक – a तथा दूसरे अर्ध समय अंतराल 0 से 1/2 तक a है।

यह जटिल फलन फूरिये प्रमेय की सभी प्रतिबन्धों को संतुष्ट करता है इसीलिये वर्गाकार तरंग के विस्थापन को निम्न फूरिये श्रेणी के रूप में लिख सकते हैं।

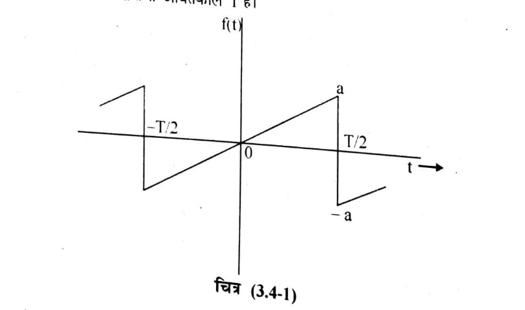
 आरादंती तरंग की फूरिये श्रेणी ( FOURIER SERIES OF SAWTOOTH WAVE) माना आरादंती तरंग की भांति किसी तरंग का विस्थापन – समय वक्र चित्र (3.4-1) में दर्शाया गया है। इसका आयाम a तथा आवर्तकाल T है ।

यह जटिल फलन फूरिये प्रमेय की सभी प्रतिबंधों का संतुष्ट करता है इसीलिये आरादंती तरंग के विस्थापन को निम्न फूरिये श्रेणी के रूप में लिख सकते हैं।

उपरोक्त समीकरण से प्रेक्षित है कि आरादंती तरंग में सभी प्रसंवादी उपस्थित होते हैं तथा उनके आयाम प्राकृतिक संख्या के व्युत्क्रमानुपाती होते हैं।

अर्ध तरंग दिष्ट्कारी में निर्गत वोल्टता की फूरिये श्रेणी (FOURIER SERIES OF OUTPUT VOLTAGE IN HALF WAVE RECTIFIER) अर्ध तरंग दिष्ट्कारी में निर्गत वाल्टता को चित्र (3.5-1) मं दर्शाया गया है जिसे गणितीय रूप में निम्न समीकरण द्वारा निरूपित कर सकते हैं।

अर्ध तरंग दिष्ट्कारी में निर्गत वोल्टता वक्र फलन फूरिये प्रमेय की सभी प्रतिबंधों को संतुष्ट करता है इसीलिये अर्ध तरंग के विस्थापन को निम्न फूरिये श्रेणी के रूप में लिख सकते हैं।

पूर्ण तरंग दिष्टकारी में निर्गत वोल्टता की फूरिये श्रेणी (FOURIER SERIES OF OUTPUT VOLTAGE IN FULL WAVE RECTIFIER) पूर्णतरंग दिष्ट्कारी में निर्गत वोल्टता निवेश वोल्टता के पूर्ण आवर्त काल के लिये प्राप्त होता है। जिसे चित्र (3.5-1) में दर्शाया गया है तथा गणितीय रूप में इसके वक्र को निम्न समीकरण द्वारा निरूपित कर सकते हैं।

पूर्ण तरंग दिष्ट्कारी में निर्गत वोल्टता वक्र फलन फूरिये प्रमेय की सभी प्रतिबंधों को संतुष्ट करता है इसीलिये पूर्ण तरंग के विस्थापन को निम्न फूरिये श्रेणी के रूप में लिख सकते हैं।

अर्थ तरंग निर्गत वोल्टता समीकरण (2) के लिये फुरिये श्रेणी पिछले खण्ड की भांति ज्ञात कर सकते हैं। अतः अर्ध तरंग सनीकरण (2) के लिये गुणांक

इन गुणांकों का फूरिये श्रेणी में रखने पर

चूँकि समीकरण ( 5 ) समीकरण ( 2 ) के समान है इसीलिये इसके फूरिये श्रेणी को समान अन्तराल के लिये समीकरण ( 5 ) का भी फूरिये श्रेणी लिख सकते हैं। अत

समीकरण (5) तथा (6) का योग करने पर, पूर्ण तरंग दिष्टकारी में निर्गत वोल्टता का फूरिय श्रेणी,

 फूरिये श्रेणी का सम्मिश्र रूप (COMPLEX FORM OF FOURIER SERIES)

हम जानते हैं कि फूरिये श्रेणी

हम जानते हैं कि गुणांक A तथा B होते हैं.

फूरिये समाकल प्रमेय ( FOURIER INTEGRAL THEOREM) 

समय अंतराल – T / 2 << T / 2 के बीच किसी फलन f ( t) को फूरिये श्रेणी के रूप में निम्न प्रकार लिखा जा सकता है।

v

अत: जैसे-जैसे T में वृद्धि होती है उनका आवृती अंतराल कम होता जाता है तथा अंतर सूक्ष्म हो जाता है। इस आवृती अंतराल को सुविधा के लिये dw लिख सकते हैं। यह बताता है कि जैसे-जैसे ‘T अनंत की ओर अग्रसर होता है तो dw शून्य की ओर अग्रसर होता है।

समीकरण (2) में रख कर, तब इसे समीकरण (1) में रखने पर,

उपरोक्त तथ्य को ध्यान में रखते हुए, जैसे- जैसे T → ० हम सूक्ष्म (w को dw तथा no का (क्योंकि n बहुत बड़ी संख्या है) तथा संकलन चिन्ह को सभी आवृत्तियों के लिये समाकलन चिन्ह में परिवर्तित कर सकते हैं। अतः

………(4)

ब्रेकेट के अंदर t के सापेक्ष समाकलन से (w ) पर निर्भर फलन प्राप्त होता है जिसे फलन F(w) लिख सकते हैं अर्थात्

फलन F(w) फलन f(t) का फूरिये रूपांतर (Fourier transform) तथा फलन f (t) को प्राय: फलन F(w) का प्रतिलोम फूरिये रूपांतर (inverse fourier transform) कहते हैं ।