elastic collision of two particles in hindi definition formula दो कणों की अप्रत्यास्थ टक्कर क्या है
दो कणों की अप्रत्यास्थ टक्कर क्या है elastic collision of two particles in hindi definition formula ?
अध्याय : आपेक्षिकीय गतिकी (Relativistic Dynamics)
चतुर्विम संवेग संरक्षण (FOUR-MOMENTUM CONSERVATION)
जब कोई दो कण या पिण्ड एक दूसरे की ओर गति करते हैं या निकट आते हैं यदि उनके संवेग या ऊर्जा या दोनों में पारस्परिक अन्योन्य क्रिया द्वारा परिवर्तन होता है तो इस अन्योन्य क्रिया को दो कणों या पिण्डों की टक्कर कहते हैं। टक्कर में यह आवश्यक नहीं है कि वे एक दूसरे को स्पर्श करें बल्कि वे एक दूसरे को प्रभावित करने चाहिए।
दो बिन्दुवत् द्रव्यमान कणों के टक्कर में टक्कर से पूर्व उनकी कुल ऊर्जा (विराम द्रव्यमान ऊर्जा + गतिज ऊर्जा) तथा संवेग टक्कर के पश्चात कुल ऊर्जा एवं संवेग के योग के बराबर होती है अर्थात् संयुक्त रूप से कुल ऊर्जा तथा संवेग टक्कर के दौरान निश्चर रहती है इसे चतुर्विम संवेग के संरक्षण का नियम कहते हैं क्योंकि चतुर्विम संवेग का चतुर्थ घटक कुल ऊर्जा को व्यक्त करता है जबकि अन्य घटक आकाशीय घटक को प्रदर्शित करते हैं।
माना किसी निर्देश तंत्र S में दो बिन्दुवत् द्रव्यमान कण टक्कर करते हैं। टक्कर से पूर्व उनके चतुर्विम संवेग P3u एवं P2u तथा टक्कर के पश्चात् उनके चतुर्विम संवेग क्रमश: P3 एवं P4 हैं। चतुर्विम संवेग के संरक्षण के नियमानुसार,
चूँकि ऊर्जा एवं संवेग दो पृथक राशियाँ हैं अतः चतुर्विम संवेग का चतुर्थ घटक ऊर्जा के संरक्षण के नियम को व्यक्त करता है जबकि चतुर्विम संवेग के शेष तीनों घटक संवेग के संरक्षण के नियम को व्यक्त करते हैं।
अब एक अन्य निर्देश तंत्र S’ जो निर्देश तंत्र S के सापेक्ष + X अक्ष के अनुदिश नियत वेग v से गतिशील है, में दो कणों के टक्कर को प्रेक्षित करते हैं। माना निर्देश तंत्र S’ में इन कणों के टक्कर से पूर्व चतुर्विम संवेग P1u एवं P2u तथा टक्कर के पश्चात् संवेग क्रमश: P3u एवं P4u है। निर्देश तंत्र S से तंत्र S’ में चतुर्विम संवेग के रूपान्तरण समीकरण के आधार पर लिख सकते हैं-
चूँकि निर्देश तंत्र S में चतुर्विम संवेग के संरक्षण का नियम वैध है इसलिये निर्देश तंत्र भी चतुर्विम संवेग के संरक्षण का नियम वैध रहेगा। अतः चतुर्विम संवेग सभी जड़त्वीय निर्देश तंत्रों में संरक्षित रहता है।
प्रयोगशाला एवं द्रव्यमान केन्द्र निर्देश तंत्रों के बीच रूपान्तरण (TRANSFORMATION BETWEEN LABORATORY AND CENTRE OF MASS FRAMES OF REFERENCE)
(i) द्रव्यमान केन्द्र निर्देश तंत्र
यदि किसी जड़त्वीय निर्देश तंत्र का मूल बिन्दु विलगित ( बहुकणीय) निकाय के द्रव्यमान केन्द्र पर स्थित हो तो उस निर्देश तंत्र के सापेक्ष द्रव्यमान केन्द्र सदैव विरामावस्था में रहेगा अर्थात् Vc = 0। इस प्रकार के निर्देश तंत्र को द्रव्यमान केन्द्र निर्देश तंत्र या C. निर्देश तंत्र कहते हैं। द्रव्यमान केन्द्र निर्देश तंत्र में निकाय के सभी कणों का कुल रेखीय संवेग शून्य होता है क्योंकि_P=MV = 0 अर्थात् V. = 0 | इस कारण C-निर्देश तंत्र को शून्य संवेग निर्देश तंत्र भी कहते हैं।
चूँकि बाह्य बलों की अनुपस्थिति में निकाय का द्रव्यमान केन्द्र या तो विरामावस्था में होता है या नियत वेग से गति करता है इसलिये विलगित निकाय का C-निर्देश तंत्र जड़त्वीय निर्देश तंत्र होगा। प्रयोगशाला से संलग्न निर्देश तंत्र को प्रयोगशाला निर्देश तंत्र या L – निर्देश तंत्र कहते हैं। भौतिकी की कुछ समस्याओं का हल प्रयोगशाला निर्देश तंत्र में कठिन होता है परन्तु उनको C- निर्देश तंत्र में हल करना सरल हो जाता है।
माना प्रयोगशाला निर्देश तंत्र में विराम द्रव्यमान m1 के कण का संवेग p1 तथा ऊर्जा E1 है यह विराम द्रव्यमान m2 के स्थिर कण जिसकी ऊर्जा E2 है, से टक्कर, करता है C-निर्देश तंत्र में
इन कणों के संवेग तथा ऊर्जा क्रमश: P1, E1 एवं P2, E2 है। इन राशियों को चतुर्विम संवेग के संरक्षण के नियम द्वारा ज्ञात कर सकते हैं।
अतः चतुर्विम संवेग के संरक्षण के नियम से,
P1u + P2u = P’1u + P2u ………………. (1)
चूँकि C-निर्देश तंत्र में निकाय का कुल आकाशीय संवेग शून्य के बराबर होता है इसलिये
P + p2 = 0 …………………..(2)
(ii) C-निर्देश तंत्र में कणों की कुल ऊर्जा
सामान्यतया कण के चतुर्विम संवेग के निम्न चार घटक होते हैं-
जहाँ p एवं E कण के क्रमशः संवेग तथा ऊर्जा है।
समीकरण (1) का स्वयं के साथ अदिश गुणनफल लेने पर,
परन्तु हम जानते हैं कि
समीकरण (2) से, P1 + P2 = 0
C- निर्देश तंत्र में कणों की कुल ऊर्जा E’1 + E’ 2 = E’
ये सभी मान समीकरण (3) में रखने पर,
परन्तु प्रयोगशाला निर्देश तंत्र में स्थिर कण की ऊर्जा E2 = m2c2
(iii) C-निर्देश तंत्र में कणों का संवेग
C-निर्देश तंत्र की परिभाषा से, टक्कर से पूर्व कणों का कुल संवेग शून्य होता है
P1 + p2 = 0
चूँकि प्रयोगशाला निर्देश तंत्र में m2 विराम द्रव्यमान वाला कण स्थिर है इसलिये C-निर्देश तंत्र जो स्वयं Vc से गति कर रहा है, में यह कण – V वेग से गति करता हुआ प्रतीत होगा। .
निर्देश तंत्र के सापेक्ष इस कण का संवेग होगा-
समीकरण (8) व (9) को समीकरण (5) व (6) में रखने पर.
C-निर्देश तंत्र में लक्ष्य कण का संवेग,
C-निर्देश तंत्र में टक्कर करने वाले कण का संवेग,
(iv) C-निर्देश तंत्र में कणों की ऊर्जाएँ
C-निर्देश तंत्र में टक्कर करने वाले कण के संवेग ऊर्जा संबंध से
समीकरण ( 11 ) इसमें रखने पर,
प्रयोगशाला निर्देश तंत्र में टक्कर करने वाले कण के संवेग ऊर्जा सम्बन्ध से,
इस समीकरण के अंश (numerator) में समीकरण (4) से E’ का मान रखने पर,
समीकरण (4) से E1 का मान रखने पर,
इसी प्रकार C – निर्देश तंत्र में लक्ष्य कण की ऊर्जा ज्ञात कर सकते हैं।
अन आपेक्षिकीय गति (Non relativistic motion)
यदि m1 विराम द्रव्यमान वाला कण u(u<< c) वेग से गति कर रहा है तो y = 1
टक्कर करने वाले कण का संवेग p=m1u तथा ऊर्जा E1 = m1 c2
समीकरण (8) से C-निर्देश तंत्र का वेग,
C- निर्देश तंत्र में कणों की कुल ऊर्जा
समीकरण (4) से,
C- निर्देश तंत्र में कणों का संवेग
C- निर्देश तंत्र में टक्कर करने वाले कण का संवेग,
C-निर्देश तंत्र में लक्ष्य कण का संवेग,
(vi) चरम – आपेक्षिकीय गति (Ultra-ralativistic motion) जब कणों की ऊर्जायें अत्यधिक हों ताकि E >> m1c2 तथा E2>>m2c21 गति चरम आपेक्षिकीय गति कहलाती है।
C- निर्देश तंत्र में कणों की कुल ऊर्जा
समीकरण (4) से,
यह इंगित करता है कि C-निर्देश तंत्र में कणों की कुल ऊर्जा आपतित कण के ऊर्जा के वर्गमूल के समानुपाती होता है अर्थात् यदि हमें C-निर्देश तंत्र में 30 BeV ऊर्जा वाले कणों की आवश्यकता है तो प्रयोगशाला तंत्र में आपतित कण की ऊर्जा लगभग 450 BeV होनी चाहिये। अतः C-निर्देश तंत्र में अत्यधिक ऊर्जा प्राप्त करना अत्यंत कठिन कार्य होता है।
अत: समीकरण (12) एवं ( 13 ) से चरम – आपेक्षिकीय गति के लिये
अतः चरम – आपेक्षिकीय गति की स्थिति में C-निर्देश तंत्र में दोनों कणों की ऊर्जायें लगभग बराबर होती हैं।
संवेग -ऊर्जा सम्बन्ध से चरम आपेक्षिकीय गति के लिये,
दो कणों की अप्रत्यास्थ टक्कर (INELASTIC COLLISION OF TWO PARTICLES)
जब कोई दो कण टक्कर के पश्चात् या तो संयुक्त हो जाते हैं या भिन्न द्रव्यमान के कणों में परिवर्तित हो जाते हैं। इस प्रकार के टक्कर को अप्रत्यास्थ टक्कर (inelastic collision) कहते हैं। इस टक्कर में कणों की गतिज ऊर्जा संरक्षित नहीं रहती है तथा कणों की अधिकांश गतिज ऊर्जा अन्य ऊर्जाओं में जैसे ध्वनि, प्रकाश, ऊष्मा के रूप में परिवर्तित हो जाती है और इसके फलस्वरूप निकाय की ऊर्जा में ह्रास होता है परन्तु अप्रत्यास्थ टक्कर में कणों का कुल संवेग संरक्षित रहता है। । बंदूक की गोली का लक्ष्य द्वारा रोकना, प्राक्षेपिकीय लोलक (ballistic pendulum) आदि अप्रत्यास्थ टक्कर के उदाहरण हैं।
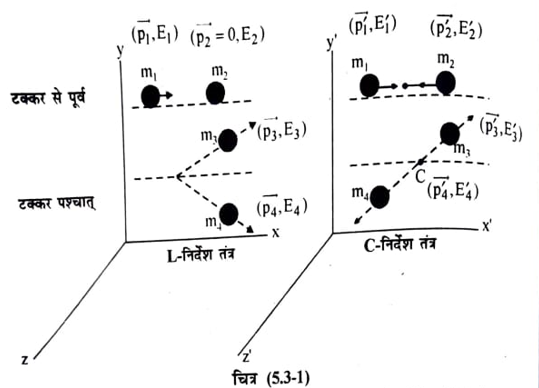
माना प्रयोगशाला निर्देश तंत्र में विराम द्रव्यमान m1 का एक गतिशील कण जिसका संवेग P1 एवं ऊर्जा E1) है, विराम द्रव्यमान m2 के स्थिर कण से टक्कर करता है और टक्कर के पश्चात् विराम द्रव्यमान m3 एवं m4 के दो कणों में परिवर्तित हो जाते हैं जिनका संवेग एवं ऊर्जा क्रमश: p3 व P4 तथा E3 व E4 हैं। अब इस टक्कर को द्रव्यमान केन्द्र निर्देश तंत्र (C-reference frame) के सापेक्ष देखते हैं। माना द्रव्यमान केन्द्र निर्देश तंत्र में टक्कर से पूर्व इन कणों का संवेग क्रमशः P1,.P2 तथा ऊर्जाएँ E’1, E’2 हैं और टक्कर के पश्चात् संवेग क्रमश: P3, P4 तथा ऊर्जाएं E3, E4 हैं।
हम जानते हैं कि चतुर्विम संवेग के संरक्षण का नियम सभी जड़त्वीय निर्देश तंत्रों में वैध रहता है और C-निर्देश तंत्र भी जड़त्वीय निर्देश तंत्र है अतः इस नियम को C-निर्देश तंत्र में उपयोग करने पर,
इस समीकरण का स्वयं के साथ अदिश गुणनफल लेने पर,
चतुर्विम संवेगों को उनके घटकों के रूप में लिखने पर,
C-निर्देश तंत्र में टक्कर के पश्चात् कणों की ऊर्जाएँ
चूँकि C-निर्देश तंत्र में टक्कर से पूर्व कणों का कुल संवेग शून्य के बराबर होता है इसलिये
इन मानों को समीकरण (1) में रखने पर,
इसी प्रकार C-निर्देश तंत्र में m4 विराम द्रव्यमान वाले कण की ऊर्जा को ज्ञात कर सकते हैं।
C- निर्देश तंत्र में टक्कर के पश्चात् कणों के संवेग
C- निर्देश तंत्र में संवेग ऊर्जा सम्बन्ध से,
इसमें समीकरण (2) रखने पर,
ये समीकरण ( 2 ) (3) (4) तथा (5) प्रत्यास्थ तथा अप्रत्यास्थ दोनों प्रकार के टक्करों के लिये वैध है परन्तु प्रत्यास्थ टक्कर के लिए m1 = m3 तथा m2 = m4 होता है।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics