THRESHOLD REACTION ENERGY in hindi देहली अभिक्रिया ऊर्जा किसे कहते हैं सूत्र क्या है परिभाषा
देहली अभिक्रिया ऊर्जा किसे कहते हैं सूत्र क्या है परिभाषा THRESHOLD REACTION ENERGY in hindi ?
C – निर्देश तंत्र से L – निर्देश तंत्र में रूपान्तरण (TRANSFORMATION FROM C-REFERENCE FRAME TO L-REFERENCE FRAME)
पिछले खण्ड से यह प्रेक्षित होता है कि C-निर्देश तंत्र में टक्करों का अध्ययन L – निर्देश तंत्र की अपेक्षा ज्यादा सुविधाजनक होता है परन्तु सामान्यतया टक्कर के प्रयोग L-निर्देश तंत्र के सापेक्ष किये जाते हैं इसलिए C- निर्देश तंत्र से L -निर्देश तंत्र में संवेग तथा ऊर्जा का रूपान्तरण आवश्यक हो जाता है।
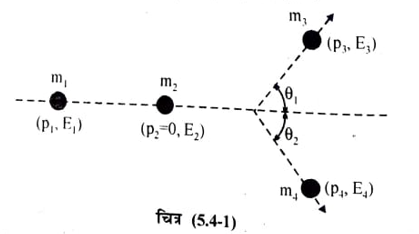
माना प्रयोगशाला निर्देश तंत्र में विराम द्रव्यमान m1 का एक गतिशील कण जिसका संवेग P1 एवं ऊर्जा E1 है, विराम द्रव्यमान m2 के स्थिर कण से टक्कर करता है और टक्कर के पश्चात् विराम द्रव्यमान m3 एवं m4 के दो कणों में परिवर्तित हो जाते हैं जिनका संवेग एवं ऊर्जा क्रमशः P3 व 14 तथा E3 व E4 हैं जैसा कि चित्र (5.4-1 ) में दर्शाया गया है। अब इस टक्कर को द्रव्यमान केन्द्र निर्देश तंत्र (C-reference frame ) के सापेक्ष देखते हैं। माना C-निर्देश तंत्र में टक्कर से पूर्व इन कणों के संवेग क्रमश: P1, P2 तथा ऊर्जाएँ E’1, E2 हैं और टक्कर के पश्चात् संवेग क्रमशः p3, P4 तथा ऊर्जाएँ E3, E4 हैं इसे चित्र (5.4-2) में दर्शाया गया है।
माना प्रयोगशाला निर्देश तंत्र में कण निकाय का द्रव्यमान केन्द्र Vc. वेग से गति कर रहा है। अत: C-निर्देश तंत्र के सापेक्ष L – निर्देश तंत्र Vcवेग आपतित कण के विपरीत दिशा में गतिमान प्रेक्षित होगा। खण्ड (5.2) के समीकरण (8) से,
संवेग -ऊर्जा सम्बन्ध के लॉरेंज रूपान्तरण से L -निर्देश तंत्र में m3 विराम द्रव्यमान वाले कण की ऊर्जा
जहाँ C-निर्देश तंत्र में m3 विराम द्रव्यमान तथा E’3 ऊर्जा वाले प्रकीर्ण कण की दिशा आपतित कण की दिशा से 0 बनाती है । खण्ड (5.2) के समीकरण ( 9 ) से,
समीकरण (3) तथा खण्ड (5.3) के समीकरण (4) से,
विराम द्रव्यमान m3 वाले कण के संवेग के x-घटक का लॉरेंज रूपान्तरण से
a का मान 1 से कम या बराबर या अधिक हो सकता है अत: समीकरण (9) तीन सम्भावनाओं को व्यक्त करता है कि,
इससे यह स्पष्ट होता है कि C-निर्देश तंत्र में जैसे-जैसे 0′ का मान 0 से तक प्रतिवर्तित होता है तो L -निर्देश तंत्र में, का मान भी 0 सेग तक प्रतिवर्तित होता है।
इससे यह स्पष्ट होता है कि C-निर्देश तंत्र में जैसे-जैसे 0 का मान 0 से तक प्रतिवर्तित होता है तो L-निर्देश तंत्र में 0 का मान 0 से 1/2 तक प्रतिवर्तित होता है। इसका अर्थ है कि L-निर्देश क्षेत्र में पश्च प्रकीर्णन (back scattering) नहीं होता है जबकि C-निर्देश तंत्र में यह प्रेक्षित किया जा सकता है।
इस स्थिति में यह प्रेक्षित किया जाता है C-निर्देश तंत्र में जैसे-जैसे 0′ का मान 0 से प्रतिवर्तित होता है तो L-निर्देश तंत्र में, 0, का मान 0 से परिवर्तित होकर फिर 0 पर ही पहुंच जाता है। इसका तात्पर्य है कि C-निर्देश तंत्र में 0 से के बीच कोई कोण ‘m होता है जिसके लिए 01 का मान उच्चतम होता है।
समीकरण ( 9 ) का अवकलन करने पर,
कोण 0’m के संगत कोण 01m का मान समीकरण ( 9 ) से ज्ञात किया जा सकता है।
अतः हम प्रेक्षित करते हैं कि a >> 1 के लिए जैसे-जैसे 0′ का मान में 0 तक वृद्धि होती है। 01 का मान 0 से 01m तक वृद्धि होती है तत्पश्चात् 0′ का मान तक वृद्धि होने पर 01) का मान शून्य की ओर अग्रसर होता है। 0′ के साथ 01 के परिवर्तन को चित्र (5.4-3) में दर्शाया गया है। इस ग्राफ से यह प्रेक्षित होता है कि C-निर्देश तंत्र में अग्र तथा पश्च प्रकीर्णित होने वाले कण L निर्देश तंत्र में एक ही कोण पर प्रकीर्णित होते दिखाई देते हैं परन्तु उन्हें उनके ऊर्जा के मान द्वारा पहचाना जा सकता है।
अस्थाई कणों के क्षय उत्पादों की गतिकी (KINEMATICS OF DECAY PRODUCTS OF UNSTABLE PARTICLES)
कुछ विशिष्ट अवस्थाओं में अस्थाई कण दो या दो से अधिक कणों में विघटित होते हैं। उदाहरण के तौर पर, r°मेसॉन (pi meson), ut मेसॉन (mu mason) तथा v न्यूट्रिनो (neutrino) में विघटित होता है तथा u` मेसॉन (mu mason), e-इलेक्टॉन (electron), v न्यूट्रिनो (neutrino) तथा प्रति न्यूट्रिनो (anti neutrino) में विघटित होता है ।
माना प्रयोगशाला निर्देश तंत्र में m विराम द्रव्यमान का एक कण जिसका संवेग शून्य है, m1तथा m2 द्रव्यमान वाले कणों में विघटित होता है जिनके संवेग क्रमश: P1 व P2 तथा गतिज ऊर्जाएँ क्रमशः T1 व T2 है। इन कणों के चतुर्विम संवेग निम्न रूप में लिख सकते हैं-
इस समीकरण के संवेग के आकाशीय घटक तथा ऊर्जा को पृथक रूप से लिखने पर.
जहाँ m = m – m1 – m2 अस्थाई कण के विराम द्रव्यमान तथा उत्पाद कणों के विराम द्रव्यमानों के बराबर होता है इसे विघटन के लिए द्रव्यमान हानि (mass loss) कहते हैं। चूँकि कणों की गतिज ऊर्जायें हमेशा धनात्मक होती है इसलिये विघटन में द्रव्यमान हानि धनात्मक होती है अर्थात्
m > (m1 + m2)
कण के स्वयं विघटन के लिये यह आवश्यक है कि अस्थाई कण का विराम द्रव्यमान उत्पाद कणों के विराम द्रव्यमानों के योग से अधिक होना चाहिए।
समीकरण (3) से,
P1u = Pu – P2u
इस समीकरण का स्वयं के साथ अदिश गुणनफल लेने पर,
समीकरण (2) तथा (7) का समीकरण (6) में उपयोग करने पर,
देहली अभिक्रिया ऊर्जा (THRESHOLD REACTION ENERGY) : जब कोई ऊर्जावान कण किसी स्थिर कण से टक्कर करता है तो यह सम्भावना हो सकती है कि इस अभिक्रिया में कई कण उत्पन्न हो जायें। अतः टक्कर करने वाले कण की न्यूनतम ऊर्जा जिससे अभिक्रिया में शून्य गतिज ऊर्जा से कई कण उत्पन्न हो जायें तो न्यूनतम ऊर्जा को देहली अभिक्रिया ऊर्जा (threshold reaction energy) ) कहते हैं। प्रयोगशाला निर्देश तंत्र में, माना विराम द्रव्यमान m1का एक कण A, जिसका संवेग PI तथा ऊर्जा E1 हैं, विराम द्रव्यमान m2 तथा ऊर्जा के E2 के स्थिर कण B से टक्कर करता है और विराम द्रव्यमान m3 एवं m4 दो कण क्रमश: C एवं D उत्पन्न करता है इसलिये
अब हम इस अभिक्रिया को C-निर्देश तंत्र में प्रेक्षित करते हैं जहाँ C-निर्देश तंत्र के सापेक्ष टक्कर से पूर्व कणों का कुल संवेग शून्य होता है अर्थात् P1 + P2 = 0 माना C-निर्देश तंत्र में विराम द्रव्यमान m1 संवेग P2 तथा ऊर्जा E’2 है। के कण A का तथा विराम द्रव्यमान m2 के कण B संवेग P2 तथा ऊर्जा E’ है
C-निर्देश तंत्र में A व B कणों का कुल चतुर्विम संवेग,
हम जानते हैं कि चतुर्विम संवेग के घटकों का योग सभी जड़त्वीय निर्देश तंत्रों में सदैव निश्चर रहता है तथा C-निर्देश तंत्र एक जड़त्वीय निर्देश तंत्र है इसलिये
इसमें समीकरण (3) तथा (4) रखने पर,
C-निर्देश तंत्र में अभिक्रिया से पूर्व A व B कणों की कुल ऊर्जा,
ऊर्जा के संरक्षण के नियमानुसार यह ऊर्जा उत्पाद कणों की कुल ऊर्जा के बराबर होती है।
उत्पाद कणों की कुल ऊर्जा
जहाँ उत्पाद कणों की गतिज ऊर्जाएँ T3 व T4 है ।
माना इस अभिक्रिया में न्यूनतम देहली ऊर्जा (threshold energy) Tth है। देहली ऊर्जा की परिभाषानुसार आपतित कण की ऊर्जा E1 = mc2 + Tth होगी जब उत्पाद कणों की गतिज ऊर्जाएँ शून्य के बराबर होती हैं। अतः
उत्पाद कणों तथा अभिक्रिया से पूर्व कणों के विराम द्रव्यमानों का अंतर है इसे द्रव्यमान आधिक्य (excess mass) कहते हैं। यह अभिक्रिया तभी सम्भव है जब द्रव्यमान आधिक्य का मान धनात्मक हो अतः
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics