फूरियर श्रेणी किसे कहते हैं परिभाषा क्या है सूत्र FOURIER SERIES definition in hindi formula
FOURIER SERIES definition in hindi formula फूरियर श्रेणी किसे कहते हैं परिभाषा क्या है सूत्र ?
फूरिये श्रेणी ( FOURIER SERIES) : यदि वाद्य यंत्रों (musical instruments) द्वारा उत्पन्न ध्वनियों के विस्थापन – समय वक्र प्रेक्षित किये जायें तो ये वक्र जटिल आवर्ती फलन (complex periodic function) के रूप में प्राप्त होते हैं। ये वक्र सरल आवर्ती फलन नहीं होते है परन्तु वे एकल मानी ( single valued ) परिमित (finite) तथा सतत (continuous) जटिल फलन होते हैं। इस प्रकार के जटिल आवर्ती फलनों के लिये 1807 में फूरिये (Fourier) ने एक प्रमेय का प्रतिपादन किया, जिसके अनुसार सभी एक मानी ( single valued), परिमित (finite ) तथा सतत ( continuous ) जटिल फलनों को अनन्त सरल आवर्ती फलनों के योग से व्यक्त कर सकते है जिसकी आवर्तियाँ जटिल फलनों की मूल आवर्ती (fundamental frequency) की पूर्ण – गुणज होती है।
सभी जटिल आवर्ती फलन निम्न गुणधर्म रखते हैं।
f(x) = f(x + P) ….(1)
चर राशी x के अनुसार P के विभिन्न मान तथा नाम होते हैं। जब चर राशी x को समय द्वारा व्यक्त करते हैं P आवर्त काल T कहलाता है। जब चर राशी x को कला कोण 0 द्वारा व्यक्त करते है तो P = 2 होता है तथा जब चर राशी x को दूरी द्वारा व्यक्त करत हैं तो P = A (तरंग द) होता है।
सभी जटिल आवर्ती फलनों को निम्न प्रकार से लिख सकते हैं।
यहाँ fe(x) एक सम फलन है जैसे cos ( – x) = cos x, अत: कोज्या फलन (cosine function) एक सम फलन होता है।
यहाँ fo(x) एक विषम फलन है जैसे sin (x): -sin x, अतः ज्या फलन (sine function ) एक विषम फलन होता है।
अतः समीकरण (3) के अनुसार, सभी जटिल आवर्ती फलनों का सदैव सम तथा विषम फलनों के योग से व्यक्त किया जा सकता है अर्थात् जटिल आवर्ती फलन को सम आवर्ती फलन ( कोज्या फलन) तथा विषम आवर्ती फलन (ज्या फलन) के श्रेणी के रूप में व्यक्त किया जा सकता है। यह श्रेणी फूरिये श्रेणी (Fourier series) कहलाती है।
यदि फलन f(x) कला कोण x = 6 का आवर्ती फलन है तथा यह 21 कोण से पुनरावर्ती करता है तो समीकरण (6) से,
अतः कला कोण के सापेक्ष फूरिये श्रेणी होगी ।
यदि फलन f(x) दूरी या विस्थापन का आवर्ती फलन है तो समीकरण (6) में x को kx = 2x/ से तथा P को 2 से प्रतिस्थापित करने पर, जहाँ तरंगदैर्ध्य है।
अत: दूरी के सापेक्ष फूरिये श्रेणी होगी ।
यदि फलन f(x) समय 1 का आवर्ती फलन है तो समीकरण (6) में x को t = 2t P को 2 से प्रतिस्थापित करने पर, जहाँ T आवर्त काल है।
समीकरण (7), (8) व (9) फूरिये श्रेणी कहलाती हैं। इन श्रेणियों में y जटिल आवर्तीफलन के विस्थापन को व्यक्त करता है तथा A1, A2, A3 एवं B1, B2,………. Bn क्रमशः कोज्या तथा ज्या फलनों के आयाम गुणांकों को व्यक्त करता है। नियतांक Ao स्थायी स्थिति से विस्थापन को व्यक्त करता है। ये सभी गुणांक फूरिये गुणांक (Fourier coefficients) कहलाते हैं तथा इन्हें जटिल आवर्तीफलन के ज्ञात प्रतिबंधों द्वारा प्राप्त कर सकते हैं।
(i) फूरिये गुणांकों का निर्धारण (Determination of Fourier coefficients)
(a) गुणांक Ao
Ao का निर्धारण करने के लिये समीकरण ( 9 ) को – T / 2 to T / 2 के बीच समाकलन करने पर, .
अतः गुणांक B के साथ संलग्न समाकल के अतिरिक्त सभी समाकल का मान शून्य होता है।
सारांश में फूरिये गुणांकों के समाकलों को लिख सकते हैं.
(ii) फूरिये श्रेणी की विशेषतायें (Characteristic of Fourier Series)
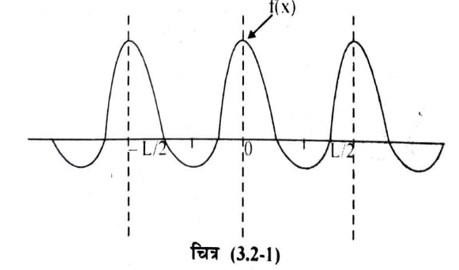
(1) फूरिये श्रेणी परिमित अंतराल के मध्य एकल मानी, परिमित एवं संतत जटिल आवर्ती फलनों का सरल आवर्ती फलनों के श्रेणी के रूप में व्यक्त करता है। इस प्रकार के आवर्ती फलन को चित्र (3.2-1 ) में दर्शाया गया है।
स्पष्टतः एकल मानी, परिमित एवं सतत जटिल आवर्ती फलन f(x) कोज्या तथा कोज्या पदों के योग के रूप में व्यक्त कर सकते हैं जिसकी आवर्तिता x = L2 = 2L2 = 3L/2 पर होती है अर्थात्
(2) सम्पूर्ण सतत फलन – फूरिये विश्लेषण आवर्तिक सतत फलनों के विश्लेषण के लिये भी उपयोग में ला सकते हैं। के बीच आवृती वर्णक्रम
,को विवक्त लेन हुये आवर्तिक वक्रों का विश्लेषण करने के स्थान पर, आवृत्ति वर्णक्रम को सतत मानकर भी बक्रा का विश्लेषण कर सकते हैं। एत्येक आवृत्ति के साथ संलग्न गुणांक आवृत्ति का फलन होता है। विश्लेषित फलन को फूरिये रूपांतर कहते हैं।
(iii) फूरिये प्रमेय के लिये प्रतिबंध
किसी जटिल आवर्ती फलन का फूरिये प्रमेय द्वारा विश्लेषण करने के लिये निम्न प्रतिबंध संतुष्ट होने चाहिये।
(1) एकल मानी (Single valued) : जटिल आवर्ती फलन एकल मानी होना चाहिये। इसका तात्पर्य है कि के किसी एक मान के लिये f (x) का एक ही निश्चित मान होना चाहिये ।
(2) परिमित (finite ) : जटिल आवर्ती फलन हमेशा परिमित होना चाहिये। इसका तात्पर्य है कि फलन का विस्थापन किसी भी समय या दूरी पर अनंत नहीं होना चाहिये
। (3) समाकलनीय (Integrable) : आवर्तिक अंतराल के बीच जटिल आवर्ती फलन समाकलनीय होना चाहिये।
(4) सतत (Continuous ) : जटिल आवर्ती फलन सतत होना चाहिये । यदि जटिल आतव फलन पूर्णत: सतत नहीं है तो (i) उच्चिष्ठ तथा निम्निष्ठ (Maxima and minima) : एक आवर्ती अंतराल में फलन के संख्या परिमित मात्रा में उच्चिष्ट तथा निम्निष्ट होने चाहिये।
(ii) असंतत्यता (Discontinuities) : एक आवर्ती अंतराल में फलन के परिमित संख्या में असंतत्यता होनी चाहिये। प्रतिबन्ध (i) तथा (ii) डिरिशले (Dirichlet) प्रतिबंध कहलाते हैं।
(5) परिबद्ध (Bounded) : जटिल आवर्ती फलन परिसीमा द्वारा परिबद्ध होना चाहिये।
(iv) माध्य वर्ग मान (Mean square value) यदि किसी जटिल आवर्ती फलन ft) का वर्ग माध्य मान ज्ञात करना हो ता माध्य परिभाषा से,
दूसरे सभी समाकल जिसमें ज्या तथा कोज्या फलनों के विभिन्न गुणज है, का मान शून्य बराबर होता है।
हम जानते हैं कि तरंग या आवर्त गति की ऊर्जा आयाम के वर्ग के समानुपाती होती है। स्पष्टतः जटिल आवर्ती फलन f(wt) के वर्ग का माध्य उस तरंग या आवर्त गति की ऊर्जा को निरूपित करेगी जिसका समीकरण y = f(wt) होता है। अत: समीकरण (18) तरंग की कुल ऊर्जा का उसके प्रसंवादी घटकों की ऊर्जा से सम्बन्ध स्थापित करता है।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics