डिराक डेल्टा फलन क्या है परिभाषा सूत्र लिखिए dirac delta function in hindi definition formula ?

अध्याय : डिराक डेल्टा फलन एवं फूरिये श्रेणी (Dirac Delta Function and Fourier Series)

डिराक डेल्टा फलन (DIRAC DELTA FUNCTION)

भौतिकी में अनेक घटनायें आवेगी प्रकृति की होती है जैसे यांत्रिकी तंत्र में हथौड़े की चोट संघट, आवेगी बल, श्रेणीबद्ध L-C परिपथ में संधारित्र का क्षणिक आवेशन आदि । ऐसी घटनाओं की गणितीय व्याख्या के लिये एक ऐसे फलन का उपयोग करते हैं जो किसी विशिष्ट समय पर सूक्ष्म समय अंतराल के लिये शून्येतर (Non- zero) हो तथा अन्य समयों के लिये शून्य हो । ऐसे फलनों को डेल्टा फलन कहते हैं जिसे डिराक ने सर्वप्रथम क्वांटम यांत्रिकी की समस्याओं को हल करने के लिये उपयोग में लिया था इसीलिये इस फलन को डिराक डेल्टा फलन भी कहते हैं।

यद्यपि यह यथार्थ फलन नहीं है परन्तु इस फलन का मान केवल विशिष्ट स्थान या समय के अतिरिक्त सर्वत्र शून्य माना जाता है, इस पर इसका मान अनंत माना जाता है अर्थात्

तथा जो निम्न शर्त को संतुष्ट करता हो ।

प्रथम समीकरण के अनुसार यह फलन x के विशिष्ट मान x = 0 पर शिखर मान (peak value) प्रदान करता है तथा समीकरण (2) के अनुसार, यह फलन x = 0 पर तीक्ष्ण वक्र (sharp curve) प्रदान करता है जिसकी चौड़ाई घटने पर ऊँचाई इस प्रकार बढ़ती है कि तीक्ष्ण वक्र द्वारा सीमित ( confined ) क्षेत्रफल सदैव एकांक हो जैसे कि चित्र (3.1-1 ) में दर्शाया गया है।

(i) डिराक डेल्टा फलन आवृत्ति फलन के रूप में,

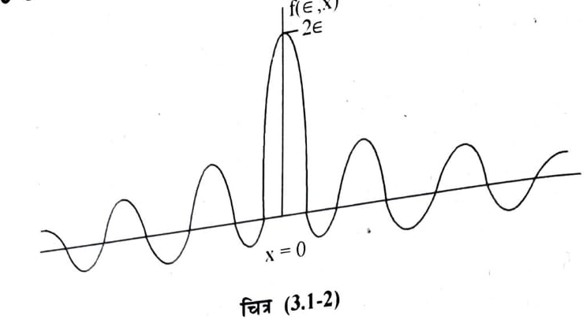
यह फलन आवृत्ति फलन होता है जिसकी आवृत्ति 1/∈ तथा शिखर मान x = 0 पर 2∈ होता है जैसा कि चित्र (3.1-2) में दर्शाया गया है।

अतः x → 0 पर शिखर वक्र तीक्ष्ण हो जाता है तथा अनंत की ओर अग्रसर होता है जैसे-जैसे ∈ का मान अनंत होता जाता है। वक्र द्वारा सीमित क्षेत्रफल एकांक रहता है।

अतः समीकरण (3a) तथा (3b) से स्पष्ट है कि यह फलन डिराक डेल्टाफलन की भांति व्यवहार करता है अर्थात्

(ii) डिराक डेल्टा फलन गॉस फलन के रूप में,

जहाँ एक वास्तविक तथा धनात्मक संख्या है। x = 0 पर इस फलन के वक्र का शिखर मान होता है।

अतः हम देखते है कि यह फलन के सभी गुणधर्मों का पालन करता है । इसलिये

(iii) डिराक डेल्टा फलन एकांक के फूरिये फलन के रूप में,

(x) को एकांक का फूरिये रूपांतर (Fourier transform) माना जा सकता है अर्थात्

इसका व्युत्क्रम फूरिये रूपांतर है,

समीकरण (6) में 8(x) के स्थानांतरी ( shifting ) गुण का उपयोग करने पर,

इसी प्रकार त्रिविमीय आकाश के लिये,

डिराक डेल्टा फलन के गुणधर्म

(i) डिराक डेल्टा फलन सम फलन होता है, अर्थात्

समीकरण (2) से,

(v) सोपानी तथा सममित (Scaling and symmetry) गुण,

माना स्वैच्छिक फलन f(x) का समाकल निम्न है

(vi) स्थानांतरी (Shifting property )

डिराक डेल्टा फलन का एक अन्य गुण स्थानांतरी गुण होता हे जिसके द्वारा इस फलन को मूल बिन्दु x = 0 से किसी अन्य बिन्दु xx’ पर स्थानांतरित किया जा सकता है अर्थात्

समीकरण (13) में स्थानांतरी गुण का उपयोग करने पर