अविरतता का सिद्धांत (सांतत्यता समीकरण) (equation of continuity in hindi)

SbistudyOctober 20, 2018inphysics

(equation of continuity in hindi) अविरतता का सिद्धांत (सांतत्यता समीकरण) : इस सिद्धांत के अनुसार “जब किसी नली में तरल का प्रवाह नियत हो तो एक निश्चित समयान्तराल में नली में प्रवेश करने वाले तरल का द्रव्यमान , उसी समयान्तराल में नली से निकलने वाले तरल के द्रव्यमान के बराबर होता है ”
यह नियम तरल गतिकी में द्रव्यमान संरक्षण नियम पर आधारित होता है।
अत: किसी तरल का प्रवाह इस प्रकार होना चाहिए कि इसमें द्रव्यमान संरक्षित रहे , यहाँ द्रव्यमान संरक्षण का नियम यह बताता है कि द्रव्यमान को न तो उत्पन्न किया जा सकता है और न ही नष्ट किया जा सकता है।
इसलिए जब तरल का प्रवाह नियत हो तो नली में जितना द्रव्यमान का तरल प्रवेश करता है उतना ही तरल द्रव्यमान बाहर निकलता है , इसमें द्रव्यमान संरक्षण रहता है।

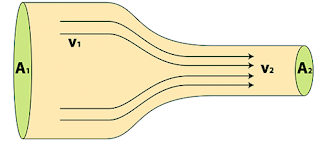
उदाहरण और सूत्र : माना चित्रानुसार कोई नली है जिसका प्रवेश द्वार का अनुप्रस्थ क्षेत्रफल A₁ है और निकास द्वार का क्षेत्रफल A₂ है। प्रवेश द्वार पर द्रव का वेग V₁ है तथा द्रव V₂ से से बाहर निकलता है , द्रव का घनत्व p है और इसे t समयांतराल तक प्रवाह किया जाता है अत:
नली में t समय में प्रवेश करने वाले द्रव का द्रव्यमान = p tV₁A₁
नली में t समय में बाहर निकलने वाले द्रव का द्रव्यमान =p t V₂ A₂
चूँकि द्रव्यमान संरक्षण के नियम से या अविरतता का सिद्धांत के अनुसार नली में प्रवेश करने वाले द्रव का द्रव्यमान , बाहर निकलने वाले द्रव के द्रव्यमान के बराबर है अत:
p tV₁A₁= p t V₂ A₂
अत:
V₁A₁= V₂ A₂
अत: यही कारण होता है कि किसी नली या पाइप के चौड़े भाग से द्रव का वेग कम होता है और संकरे भाग से द्रव का वेग अधिक होता है , यही कारण है कि जब नली का मुंह थोडा दबा लिया जाता है तो इसका पानी अधिक वेग से और अधिक दूरी तक जाता है।