कार्य क्या है , परिभाषा , प्रकार , work in hindi उदाहरण , ऊर्जा किसे कहते है , गतिज और स्थितिज ऊर्जा , प्रमेय

(what is work in hindi definition and meaning) कार्य क्या है , ऊर्जा किसे कहते है ? प्रकार और उदाहरण |

कार्य की परिभाषा : जब किसी वस्तु पर पर बल लगाया जाता है तो उस वस्तु में कुछ विस्थापन उत्पन्न हो जाता है , वस्तु पर लगाये गए बल तथा उत्पन्न विस्थापन के अदिश गुणनफल को वस्तु पर कृत कार्य कहते है।
माना वस्तु पर F बल लगाया जाता है , F बल लगाने से वस्तु में S विस्थापन उत्पन्न हो जाता है तो बल द्वारा उस वस्तु पर किया गया कार्य (W)
W = F.S होगा।

अभी तक के अध्ययन में हमने यह माना है कि बल जिस दिशा में लग रहा है विस्थापन उसी दिशा में उत्पन्न हो रहा है।
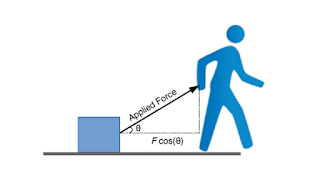
मान लीजिये विस्थापन बल की दिशा में उत्पन्न नहीं हो रहा अर्थात किसी वस्तु पर चित्रानुसार बल एक θ परआरोपित हो रहा है तथा विस्थापन क्षैतिज में उत्पन्न हो रहा है तो ऐसी स्थिति में विस्थापन की दिशा में घटक को लिया जाता है और विस्थापन व विस्थापन की दिशा में बल के घटक को गुणा करके कार्य की गणना की जाती है।

माना चित्रानुसार F बल किसी वस्तु पर θ कोण से लगाया जाता है जिससे वस्तु में क्षैतिज में S विस्थापन उत्पन्न हो जाता है।
तो किया गया कार्य
W = S.Fcosθ
कार्य एक अदिश राशि है और कार्य ज्ञात करने के लिए बल तथा विस्थापन के मध्य अदिश गुणनफल ही किया जाता है।
कार्य का मात्रक जूल (joule) होता है।

विशेष स्थितियाँ

1. यदि बल और विस्थापन दोनों एक ही दिशा में हो तो यहाँ θ = 0 होगा अत: कार्य W = F.S होगा।

2. यदि बल और विस्थापन विपरीत दिशा में हो तो यहाँ θ = 180 डिग्री होगा अत: W = -F.S होगा, अर्थात कार्य ऋणात्मक होगा।

3. यदि बल और विस्थापन लम्बवत हो अर्थात θ = 90 डिग्री हो तो W = 0 अर्थात कार्य का मान शून्य होगा।

ऊर्जा (energy)

“किसी भी वस्तु द्वारा कार्य करने की क्षमता को ही ऊर्जा कहते है। “

किसी भी वस्तु की उर्जा का मापन कार्य के रूप में किया जाता है अर्थात किसी भी वस्तु का वह कार्य ज्ञात किया जाता है जो वह अन्त तक कर सकती है और यह सम्पूर्ण कार्य ज्ञात करने के बाद उस वस्तु की ऊर्जा को बताया जाता है।

ऊर्जा का मात्रक भू जुल होता है , इसके अलावा किलोवाट घंटा (kWh) और इलेक्ट्रॉन वाट (eV) भी मात्रक है।

गतिज ऊर्जा (kinetic energy) : प्रत्येक गतिशील वस्तु में इसकी गति के कारण एक ऊर्जा निहित होती है , इस ऊर्जा को ही गतिज ऊर्जा कहते है।

गतिज ऊर्जा का मापन के लिए किसी वस्तु के गति प्रारम्भ होने से लेकर विराम अवस्था में आने तक का सम्पूर्ण कार्य ज्ञात करते है , वही उसकी गतिज उर्जा के रूप में होता है।

स्थितिज ऊर्जा (Potential energy) : जब किसी कण या वस्तु की किसी संरक्षी बल क्षेत्र में रखा जाता है तो वस्तु की स्थिति और अभिविन्यास के कारण उस वस्तु में एक ऊर्जा निहित हो जाती है , इस ऊर्जा को ही स्थितिज ऊर्जा कहते है।

स्थितिज ऊर्जा का मान ज्ञात करने के लिए किसी बल क्षेत्र में वस्तु द्वारा अपनी एक स्थिति में दूसरी स्थिति परिवर्तन में किये गए कार्य के आधार पर किया जाता है।

कार्य – ऊर्जा प्रमेय

किसी भी वस्तु या कण पर किया गया कार्य , उस वस्तु या कण की गतिज ऊर्जा में आये परिवर्तन के बराबर होती है।

अर्थात

जब किसी वस्तु पर बल लगाया जाता है अर्थात कार्य किया जाता है तो वस्तु गतिशील अवस्था में परिवर्तन करती है , जिससे वस्तु की गतिज ऊर्जा में परिवर्तन होगा , वस्तु की गतिज ऊर्जा में आया परिवर्तन वस्तु पर किये कार्य के बराबर होगा।

शोर्ट नोट्स फॉर IIT और NEET

कार्य :

W = बल x बल की दिशा में विस्थापन

W = F.s

W = F.s cosθ

बल विस्थापन वक्र : जब परिवर्ती बल F के द्वारा किसी पिंड को x₁ से x₂ तक विस्थापित किया जाता है तब किया गया कार्य –

W = _x1∫^x2 F.dx , छायांकित क्षेत्र का क्षेत्रफल

(i) संरक्षी बल : जब किसी बल के विरुद्ध वस्तु को ले जाने में किया गया कार्य वस्तु की प्रारंभिक एवं अंतिम स्थिति पर निर्भर करता है , पथ की प्रकृति पर नहीं , तो इस बल को संरक्षी बल कहते है।

संरक्षि बल के उदाहरण : गुरुत्वाकर्षण बल , चुम्बकीय बल , स्थिर विद्युत बल आदि संरक्षी बल है।

(ii) असंरक्षी बल : जब किसी बल के विरुद्ध वस्तु को ले जाने में किया गया कार्य वस्तु की प्रारम्भिक स्थिति तथा अंतिम स्थिति पर निर्भर नहीं करता है बल्कि पथ की प्रकृति पर निर्भर करता है तो इस बल को असंरक्षी बल कहते है।

असंरक्षी बल के उदाहरण : घर्षण बल , श्यान बल असंरक्षी बल के उदाहरण है।

W = (F-x) ग्राफ और विस्थापन अक्ष के मध्य का क्षेत्रफल।

(iii) किसी कमानी को खींचने पर प्रत्यानयन बल के विरुद्ध किये गए कार्य का मान –

_W= △ABC

W = Kx²/2

SI पद्धति में कार्य का मात्रक = जूल

CGS पद्धति में कार्य का मात्रक = अर्ग

1 जूल = 10⁷ अर्ग

कार्य ऊर्जा प्रमेय : इस प्रमेय के अनुसार किसी बल द्वारा किया गया कार्य वस्तु की गतिज ऊर्जा में परिवर्तन के बराबर होता है।

W = K_f – K_i

W = mv²/2 – mu²/2

यहाँ K_f वस्तु की अंतिम गतिज ऊर्जा और K_i वस्तु की प्रारंभिक गतिज ऊर्जा है।

ऊर्जा संरक्षण का नियम : इस नियम के अनुसार , ऊर्जा को न तो उत्पन्न किया जा सकता है तथा न ही नष्ट किया जा सकता है , केवल उसका रूपांतरण होता है।

अत: किसी विलगत निकाय की सम्पूर्ण ऊर्जाओं का कुल योग नियत रहता है। यह प्रकृति का मूलभूत नियम है।

शक्ति :

किसी वस्तु की कार्य करने की दर को शक्ति कहते है।

P = W/t

यदि बल के कारण वस्तु v वेग से चलती , तो शक्ति

P = बल x वेग

P = F x v

तात्कालिक शक्ति –

P_{तात्कालिक}= dW/dt

= F.v

= F.v.cosθ

गतिज ऊर्जा :

(i) v वेग से गतिमान m द्रव्यमान की वस्तु की गतिज ऊर्जा

E = mv²/2

E = (संवेग)²/2xद्रव्यमान

E = p²/2m

(ii) घूमते हुए पिंड की गतिज ऊर्जा = रेखीय गतिज ऊर्जा + घूर्णी गतिज ऊर्जा

E = mv²/2 + Iw²/2

(iii) दो वस्तुओं के संवेग समान होने पर –

E₁/E₂ = m₁/m₂

(iv) दो वस्तुओं की गतिज ऊर्जा समान होने पर –

P₁/P₂ = √m₁/√m₂

स्थितिज ऊर्जा :

प्रत्यास्थ स्थितिज ऊर्जा = Kx²/2

गुरुत्वीय स्थितिज ऊर्जा = mgh = -GMm/r

स्थितिज ऊर्जा और कार्य में सम्बन्ध △U = -△W

स्थितिज ऊर्जा और संरक्षी बल में सम्बन्ध –

F = -dU/dr

= -(U-r) वक्र की ढाल

प्रश्न और उत्तर

प्रश्न 1. एक ग्राम और चार ग्राम द्रव्यमान की दो वस्तुएं समान गतिज ऊर्जा से गतिमान है। उनके संवेगों का अनुपात है –

(a) 4:1

(b) √2 : 1

(d) 1:16

प्रश्न 2. निश्चित शक्ति देने वाली मशीन द्वारा एक पिण्ड को सरल रेखा के अनुदिश चलाया जाता है। समय t में पिंड द्वारा चली गयी दूरी अनुक्रमानुपाती है –

(a) t^1/2

(b) t^3/4

(d) t²

प्रश्न 3. एक समरूप जंजीर , जिसकी लम्बाई L और द्रव्यमान M है , एक चिकनी मेज पर पड़ी हुई है और उसकी एक तिहाई लम्बाई उर्ध्वाधर निचे की तरफ मेज के किनारे लटकी है। यदि g गुरुत्वीय त्वरण है तो इस नीचे लटके भाग को ऊपर खींचने के लिए आवश्यक कार्य होगा –

(a) MgL

(b) MgL/3

(d) MgL/18

प्रश्न 4. एक कण जिसका द्रव्यमान m है , r त्रिज्या के वृत्तीय पथ में इस प्रकार भ्रमण कर रहा है कि उसका अभिकेन्द्र त्वरण a_c समय t के साथ समीकरण a_c = k²rt² (जहाँ k एक नियतांक है ) के अनुसार परिवर्तित होता है। कण पर कार्य करने वाला बल द्वारा कण को प्रदत्त शक्ति है।

(a) 2πmk²r²

(b) mk²r²t

(d) शून्य

प्रश्न 5. L लम्बाई की एक डोरी से बंधा पत्थर उर्ध्वाधर वृत्त में इस प्रकार घुमाया जाता है जबकि डोरी का दूसरा सिरा वृत्त के केंद्र पर रहता है। किसी निश्चित समय पर जब पत्थर निम्नतम स्थिति में है , उसकी चाल u है। डोरी की क्षैतिज अवस्था में पत्थर के वेग में परिवर्तन का परिमाण है।

(a) √u² – 2gL

(b) √2gL

(d) √2(u²– gL)

प्रश्न 6. xy तल में गतिमान एक कण पर एक बल F = -k (yi + xj) (जहाँ k एक धनात्मक नियतांक है) कार्य करता है। मूल बिंदु से प्रारंभ करते हुए पहले कण को धन x अक्ष की दिशा में बिंदु (a , 0) तक ले जाया जाता है , पुनः y अक्ष के समान्तर बिंदु (a , a) तक ले जाया जाता है। कण पर बल F द्वारा किया गया कार्य है –

(a) -2ka²

(b) 2ka²

(d) ka²

प्रश्न 7. k बल नियतांक की एक स्प्रिंग को , दो भागों में इस प्रकार काटा जाता है कि एक भाग की लम्बाई दूसरे भाग की लम्बाई से दोगुनी है। लम्बे भाग का बल नियतांक होगा।

(a) (2/3)k

(b) 3/2 k

(d) 6k

प्रश्न 8. एक पवन शक्ति जनित्र पवन ऊर्जा को विद्युत ऊर्जा में परिवर्तित करता है। यह मानते हुए कि जनित्र अपने पंखो द्वारा अवरुद्ध पवन के एक निश्चित भाग को वैद्युत ऊर्जा में परिवर्तित करता है , वायु की गति v के लिए निर्गत वैद्युत शक्ति समानुपाती होगी –

(a) v के

(b) v² के

(d) v⁴के

प्रश्न 9. एक आदर्श स्प्रिंग जिसका स्प्रिंग नियतांक k है छत से लटकाया गया है और स्प्रिंग के निचले सिरे पर M द्रव्यमान का एक ब्लॉक जोड़ा गया है। प्रारंभ में स्प्रिंग खिंची अवस्था में नहीं है , द्रव्यमान M को मुक्त कर देने पर स्प्रिंग में उत्पन्न अधिकतम विस्तार है –

(a) 4Mg/k

(b) 2Mg/k

(d) Mg/2k

उत्तरमाला :