woodward fieser rule in hindi वुडवर्ड एवं फाइजर का नियम क्या है फिजर समझाइये उदाहरण सहित
वुडवर्ड एवं फाइजर का नियम क्या है फिजर समझाइये उदाहरण सहित
डाइईनों के अवशोषण के संदर्भ में वुडवर्ड एवं फ़ीजर का नियम (Woodword and Fieser’s rule for diene absorption) – विभिन्न एकल प्रतिस्थापियों के द्वारा 13 – ब्यूटाडाइईन में प्रतिस्थापन कराने पर कितना वर्णोंत्कर्षी विस्थापन होता है, इस संदर्भ में वुडवर्ड एवं फ़ीइजर ने कुछ नियम प्रतिपादित किए। उनके अनुसार 13 – ब्यूटाडाइईन को प्रारूपिक या मूल मानते हुए इसके अवशोषण के लिए मूल मान 217nm मानते हैं। 1,3 – ब्यूटाडाइईन के किसी भी कार्बन परमाणु पर स्थित हाइड्रोजन परमाणु को मेथिल समूह द्वारा प्रतिस्थापित करने पर λmax(मूल मान) में Snm का वर्णोंत्कर्षी विस्थापन जोड़ देते हैं। उदाहरणार्थ- 2.3 – डामेथिल – 1, 3 – ब्यूटाडाइईन के लिए λmax को निम्न प्रकार परिकलित करेगें ।
यौगिक के लिए मूल मान (λmax) = 217 nm
2 हाइड्रोजन परमाणुओं का 2 मेथिल समूहों से प्रतिस्थापन से उत्पन्न वर्णोंत्कर्षी विस्थापन = 2 x 5
= 10nm
अतः अवशोषण के लिए कुल तरंगदैर्ध्य λmax = 217 + 10 = 227 nm.
प्रेक्षित मान λmax = 226 m
ब्यूटाडाइईन के दो ज्यामितीय समावयवी होते हैं- सिस (Cis) एवं ट्रांस (Trans) । ब्यूटाडाइईन के एक बन्ध (C2 – C3) के घूर्णन के कारण ये दोनों समावयवी प्राप्त होते हैं । त्रिविमीय बाधा (Steric hindrance) कम होने के कारण ट्रान्स रूप, सिस की तुलना में अधिक स्थायी होता है। यह देखा गया है कि सिस समावयवी की अपेक्षा ट्रान्स समावयवी का λmax उच्चतर तरंगदैर्घ्य पर होता है।
यौगिक में विभिन्न प्रकार के संयुग्मित द्विबंध हो सकते हैं-
(i) ऐलिसाइक्लिक संयुग्मित द्विबंध या विवृत श्रृंखला में संयुग्मित द्विबंध इसकी मूल इकाई 1.3-ब्यूटाडाइइन है जिसके लिये अधिकतम अवशोषण की तरंगदैर्घ्य λmax का मान 217 nm होता है।
(ii) समवलयाकार संयुग्मित द्विबंध (Homo annular conjugated double bonds)- यदि यौगिक मे सभी संयुग्मित द्विबंध एक ही वलय में अधिक उपस्थित हों तो उन्हें समवलयाकार या समडाइईन द्विबंध कहते हैं।
(iii) विषम वलयाकार संयुग्मित द्विबंध (Hetero annular conjugated double bonds)- यदि यौगिक में उपस्थित संयुग्मित द्विबंध दो भिन्न वलयों में उपस्थित हो तो उन्हें विषम चक्रीय संयुग्मित द्विबंध कहते हैं।
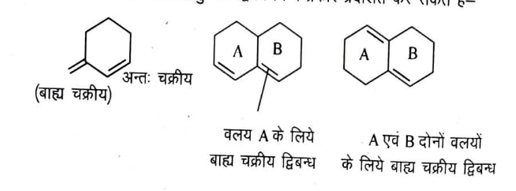
(iv) बाह्य चक्रीय एवं अन्तः चक्रीय संयुग्मित द्विबंध (Exocyclic and endocyclic conjugated double bonds)-
बाह्य चक्रीय एवं अन्तः चक्रीय संयुग्मित द्विबंध निम्न प्रकार प्रदर्शित कर सकते हैं-
निम्नलिखित तथ्यों के आधार पर किसी यौगिक के लिये λmax का मान ज्ञात कर सकते हैं-
(i) जुड़ हुये ऐल्किल समूहों तथा वलय अवशेषों के आधार पर
(ii) विभिन्न संयुग्मित द्विबंधों के आधार पर
(iii) विभिन्न ध्रुवीय समूहों CI, Br, I, OR आदि की उपस्थिति के आधार पर
विभिन्न समतलीय एवं विषमतलीय डाइईनों के अवशोषणांक ज्ञात करने के लिए कुछ अन्य नियमों को यहाँ सारणीबद्ध किया जा रहा है-
(* चक्रीय तथा विवृत श्रृंखला डाइईनों में Br तथा CI के लिये मूल मान में 17nm जोड़ते हैं)
इन नियमों के आधार पर किसी भी यौगिक के लिए अवशोषणांक का मान परिकलित किया जा सकता है।
निम्नलिखित उदाहरणों के द्वारा इस नियम को ओर अधिक स्पष्ट रूप से समझा जा सकता है-
उदाहरण 1.
(i) यह अचक्रीय यौगिक है। अतः इसके लिये Amax का मूल मान = 217 nm (ii) इसमें जुड़े ऐल्किल समूह की संख्या दो है । अतः इनके कारण Amav = 2x5nm=10nm जोड़ देंगे । (iii) इसमें वलय अवशेषों की संख्या ज्ञात करने के लिये 1,3 – ब्यूटाडाइईन की संरचना का विचार करते हुये द्विबंध के साथ जुड़ी हुई छोरों की ओर खुली संयोजकताओं की संख्याओं को गिना जाता है वह संख्या ही वलंय अवशेषों की संख्या होती है। अतः इसमें दो वलय अवशेष a एवं b होंगे। इन वलय अवशेषों का Xmas = 2 x 5 = 10nm जुड़ेगा । (iv) इसमें एक बाह्य चक्रीय द्विबंध है । अतः इसके लिये A mas = 5 nm बढ़ जायेगा ।
(* चक्रीय तथा विवृत श्रृंखला डाइईनों में Br तथा CI के लिये मूल मान में 17nm जोड़ते हैं)
इन नियमों के आधार पर किसी भी यौगिक के लिए अवशोषणांक का मान परिकलित किया जा सकता है। निम्नलिखित उदाहरणों के द्वारा इस नियम को ओर अधिक स्पष्ट रूप से समझा जा सकता है-
उदाहरण 1.
(i) यह अचक्रीय यौगिक है। अतः इसके लिये λmax का मूल मान = 217 nm
(ii) इसमें जुड़े ऐल्किल समूह की संख्या दो है । अतः इनके कारण λmax = 2 x 5nm=10nm जोड़ देंगे ।
(iii) इसमें वलय अवशेषों की संख्या ज्ञात करने के लिये 1,3 – ब्यूटाडाइईन की संरचना का विचार करते हुये द्विबंध के साथ जुड़ी हुई छोरों की ओर खुली संयोजकताओं की संख्याओं को गिना जाता है वह संख्या ही वलंय अवशेषों की संख्या होती है। अतः इसमें दो वलय अवशेष a एवं b होंगे। इन वलय अवशेषों का λmax = 2 x 5 = 10nm जुड़ेगा ।
(iv) इसमें एक बाह्य चक्रीय द्विबंध है । अतः इसके लिये λmax बढ़ जायेगा ।
अतः उपर्युक्त यौगिक में λmax का मान निम्न होगा-
(i) मूल मान = 217 nm
(ii) दो ऐल्किल समूह (2 x 5 ) = 10nm
(iii) दो वलय अवशेष (2 x 5 ) = 10nm
(iv) एक बाह्य चक्रीय द्विबंध = 5nm/242nm
(i) यह एक विषम चक्रीय संयुग्मित डाइईन है। अतः मूल मान λmax = 214nm
(ii) इसमें चार वलय अवशेष a, b, c एवं d हैं अतः इनके कारण λmax = 4 x 5 = 20 nm अतः यौगिक के λmax= 214 + 20nm = 234nm
(i) यह विषम चक्रीय संयुग्मित डाइईन है । अतः इसके लिये मूल मान λmax 214 nm
(ii) तीन वलय अवशेषों a, b, c के लिये λmax = 3 x 5 = 15 nm
(iii) बाह्य चक्रीय द्विबंध के लिये λmax = 5nm
अतः यौगिक के लिये ^ max का मान = 214 +15 + 5nm = 234 nm
(i) यदि किसी यौगिक में समचक्रीय संयुग्मित डाइन साथ विषम चक्रीय संयुग्मित डाइईन भी उपस्थित हो तो उस अवस्था में अधिक तरंगदैर्घ्य वाले मान को प्राथमिकता देते हैं।
उपर्युक्त उदाहरण में समचक्रीय संयुग्मित डाइईन का मूल मान λmax = 253nm
(ii) यदि किसी यौगिक में दो से अधिक द्विबंध उपस्थित हों तो उन्हें संयुग्मन विस्तार करने वाले द्विबंध कहते हैं । अतः प्रत्येक द्विबंध के लिये λmax = 253 nm
दो विस्तार करने वाले द्विबंधो के लिये λmax 2 x 30 = 60 nm जोड़ देगें।
(iii) पांच वलय अवशेष a, b, c, d, e के लिये λmax= 5 x 5 = 25 nm
(iv) वलय A के बाह्य चक्रीय द्विबंध के लिये λmax = 5 nm
अतः यौगिक का λmax = 253 + 60 + 25 + 5 nm = 343 nm
(i) इस यौगिक में दोनों द्विबंध विषमचक्रीय है अतः इसके लिए λmax का मान 214 m होगा ।
(ii) इस यौगिक मे तीन वलय अवशेष (a, b.c) तथा एक एकल प्रतिस्थापी d है। अतः इनके λmax 5 x 4 = 20 को Ama मूल मान में जोड़ देंगें ।
(ii) वलय A का द्विबन्ध वलय B के लिए बाह्य चक्रीय द्विबन्ध (exocyclic double bond) है। अतः इसके कारण λmax + 5 को मूल मान में जोड़ देगें।
इस प्रकार λmax का कुल मान 214 + 20+ 5 = 239nm
(i) इस यौगिक के लिए मूल मान 253nm होगा क्योंकि दोनों द्विबन्ध समचक्रीय हैं।
(ii) इस यौगिक में चार वलय अवशेष a, b, c, d हैं। अतः इनका λmax 4 x 5 = + 20 nm
(iii) इसके अतिरिक्त दोनों द्विबन्ध वलय A एवं C के लिए बाह्य चक्रीय है।
अतः इनके कारण λmax 2 x 5 = +10 nm
(iv) वलय B में संयुग्मित डाइईन के प्रतिस्थापन में एक ऐल्किल समूह का λmax = 5nm इस यौगिक का λmax का परिकलित मान = 253 + 20 + 10 +5 = 288 nm होगा।
स्वयं हल कीजिये – निम्नलिखित दो यौगिकों के λmax के मान स्वयं ज्ञात कीजिये ।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics