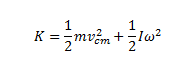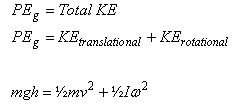WhatsApp Group Join Now

Telegram Join Join Now

लोटनी गति : क्षैतिज तल व आनत तल पर लौटनी गति क्या है , किसे कहते है , सूत्र (rolling motion in hindi)

SbistudyNovember 7, 2018inphysics

(rolling motion in hindi) लोटनी गति : क्षैतिज तल व आनत तल पर लौटनी गति क्या है , किसे कहते है , सूत्र : वाहन में लगे पहिये की गति हमने देखी है , वाहन का पहिया अपनी अक्ष के परित: घूमता रहता है और अपनी अक्ष के चारों तरफ घूमता हुआ आगे या पीछे की तरफ अर्थात रेखीय गति भी करता है , यह लोटनी गति का उदाहरण है।
परिभाषा : जब कोई वस्तु अपनी अक्ष के परित: घूर्णन गति के साथ साथ रेखीय गति भी करती है तो वस्तु की ऐसी गति को लौटनी गति कहते है।
अन्य उदाहरण : बस , कार आदि के पहिये की गति।

लोटनी गति , घूर्णन गति और रेखीय गति (स्थानान्तरीय गति) का मिला हुआ रूप है जिसमे कण दोनों प्रकार की गति एक साथ करता है।

क्षैतिज तल पर लोटनी गति (rolling motion on horizontal plane)

माना किसी क्षैतिज पर कोई पिण्ड लोटनी गति कर रहा है , इस पिण्ड का भार m है यह Vcm वेग से रेखीय गति कर रहा है तथा इसका घूर्णन गति का कोणीय वेग w है तो पिण्ड में विद्यमान कुल गतिज ऊर्जा दोनों प्रकार की गतियों के कारण होगी , अर्थात पिण्ड में गतिज ऊर्जा घूर्णन गति और स्थानान्तरीय गति दोनों के कारण होगी।

पिंड में गतिज ऊर्जा का मान –
गतिज ऊर्जा = स्थानान्तरीय गतिज ऊर्जा + घूर्णन गतिज ऊर्जा

यहाँ K = लोटनी गति कर रहे पिण्ड की कुल गतिज ऊर्जा का मान।
m = पिंड का द्रव्यमान
Vcm = रेखीय वेग
I = पिण्ड का जड़त्व आघूर्ण
w = कोणीय वेग

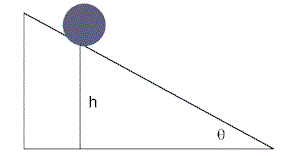
आनत तल पर लोटनी गति (rolling motion on inclined plane)

जब कोई तल किसी कोण पर झुका हुआ होता है तो ऐसे तल को आनत तल कहते है , यहाँ एक आनत तल दिखाया हुआ है जो θ कोण पर झुका हुआ है –

जब कोई पिण्ड किसी झुके हुए तल (आनत तल) से लौटनी गति करता है तो पिण्ड की ऐसी गति को आनत तल पर लोटनी गति कहते है।

माना पिण्ड आनत पर पर h ऊँचाई से छोड़ा जाता है , पिंड का द्रव्यमान m , त्रिज्या R है जो θ कोण पर झुकी आनत पर छोड़ा जा रहा है तो h ऊँचाई पर पिण्ड की स्थितिज ऊर्जा , पिंड की घूर्णन उर्जा और रेखीय गतिज ऊर्जा के योग के बराबर होगी।

पिण्ड की h ऊंचाई पर स्थितिज ऊर्जा = घूर्णन गतिज ऊर्जा + रेखीय गतिज ऊर्जा

शुद्ध लोटनी गति (अथवा बिना फिसलन के लोटनी गति)

शुद्ध लोटनी गति एक दृढ़ पिण्ड जिसका अनुप्रस्थ काट वृत्तीय है (उदाहरण – पहिया , वलय , चकती , गोला) और जो किसी सतह पर गतिमान है के सामान्य घूर्णन का एक विशेष रूप है। अत: लोटनी गति करती हुई वस्तु और स्पर्श सतह के मध्य (स्पर्श बिंदु पर) कोई सापेक्ष गति नहीं है।

स्थिति 1 : यहाँ स्पर्श बिंदु A है और स्पर्श सतह क्षैतिज धरातल है। A के शुद्ध लोटनी वेग के लिए = 0

V_A = 0

स्थिति 2 : ऊपर दिए गए चित्रानुसार शुद्ध लोटनी गति हेतु A का वेग प्लेटफार्म के सापेक्ष शून्य है।

V_A = V

स्थिति 3 : उपरोक्त चित्र से शुद्ध लोटनी गति हेतु A का वेग धरातल के सापेक्ष शून्य है।

V – wr = 0

V = wr

इसी तरह a = αr

प्रश्न : चित्रानुसार एक r त्रिज्या का पहिया एक समान सडक पर लोटनी गति करता है (बिना फिसलन के लोटनी गति) बिंदु A और B के वेग ज्ञात करो ?

उत्तर : शुद्ध लोटनी गति हेतु स्पर्श सतह विराम में है।

बिंदु A का वेग शून्य है।

अत: V = wr

बिंदु B का वेग = v + wr = 2v

दृढ़ पिण्ड की सामान्य गति की बल गतिकी

इस गति को द्रव्यमान केंद्र के स्थानान्तरण और द्रव्यमान केन्द्र से पारित अक्ष के सापेक्ष घूर्णन के रूप में भी देखा जा सकता है।

I_CM = द्रव्यमान केंद्र से पारित इस अक्ष के सापेक्ष जड़त्व आघूर्ण

τ_CM = द्रव्यमान केंद्र से पारित इस अक्ष के सापेक्ष बलाघूर्ण

a_CM= द्रव्यमान केंद्र का त्वरण

v_CM = द्रव्यमान केंद्र का वेग

F_ext = निकाय पर कार्यरत कुल बाह्य बल

P_system = निकाय का रेखीय संवेग

L_CM = द्रव्यमान केन्द्र के सापेक्ष कोणीय संवेग

r_CM = द्रव्यमान केन्द्र का बिंदु A के सापेक्ष स्थिति सदिश

तो

(1) τ_CM = I_CMα

(2) F_ext = Ma_CM

(3) P_system = Mv_CM

(4) कुल K.E. = MV²_CM/2 + I_CMw²/2

(5) L_CM = I_CMw

(6) बिंदु A के सापेक्ष कोणीय संवेग = L द्रव्यमान केन्द्र के सापेक्ष + L का द्रव्यमान केंद्र A के सापेक्ष

L_A = I_CMw + r_cm x MV_CM

dL_A/dt = d(I_CMw + r_cm x MV_CM)/dt ≠ I_Adw/dt

ध्यान दे कि बलाघूर्ण की समीकरण किसी भी दृढ़ पिण्ड के लिए सामान्य गति में केवल और केवल द्रव्यमान केंद्र से पारित अक्ष के सापेक्ष लागू कर सकते है।

प्रश्न : 200 ग्राम द्रव्यमान का समरूप गोला बिना फिसले समतल सतह पर लुढ़क रहा है। इसके द्रव्यमान केंद्र की चाल 2 cm/sec है। इसकी गतिज ऊर्जा ज्ञात करो ?

उत्तर : चूँकि गोला बिना फिसले समतल सतह पर लुढ़क रहा है तो केन्द्र के सापेक्ष इसकी कोणीय चाल w = v_CM/r है।

कुल K.E. = MV²_CM/2 + I_CMw²/2

= 5.6 x 10^-5 J (हल करने पर)

प्रश्न : m द्रव्यमान का गोला खुरदरे क्षैतिज तल पर रखा है। इसके शीर्ष बिंदु पर F स्पर्श रेखीय बल कार्यरत है। यदि गोला बिना फिसले लुढकता है तो गोले के केंद्र का त्वरण ज्ञात करो ?

उत्तर : स्थिति चित्र से स्पष्ट है जैसे ही गोले पर बल F कार्य करता है तो इसका सम्पर्क बिंदु बायीं ओर फिसलना शुरू कर देता है। जिससे गोले पर स्थैतिक घर्षण बल आगे की ओर (दाई ओर) लगने लगता है। माना गोले की त्रिज्या r है और इसके केंद्र का रेखीय त्वरण a है। चूँकि यहाँ फिसलन नहीं हो रही है अत: गोले के केंद्र के सापेक्ष कोणीय त्वरण α = a/r है।

केन्द्र के रेखीय वेग के लिए

F + f = ma . . . . . . . समीकरण-1

और केन्द्र के सापेक्ष घूर्णन गति Fr – fr = Iα = (2mr²/5)(a/r)

या

F – f = 2ma/5 . . . . .. समीकरण-2

समीकरण-1 और समीकरण-2 से

2F = 7ma/5

या

a = 10F/7m

प्रश्न : एक R त्रिज्या , m द्रव्यमान और K घूर्णन त्रिज्या वाला वृत्तीय दृढ पिण्ड एक θ कोण वाले नत तल पर बिना फिसलन के लोटनी गति करता है। दृढ पिण्ड पर घूर्णन बल और पिण्ड का रेखीय त्वरण ज्ञात करो। घर्षण गुणांक का न्यूनतम मान क्या होना चाहिए जिससे कि दृढ पिण्ड बिना फिसलन के शुद्ध लोटनी गति कर सके ?

उत्तर : न्यूनतम घर्षण गुणांक = u_min = tanθ/[1 + R²/K²]