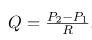हमारी app डाउनलोड करे और फ्री में पढाई करे
WhatsApp Group Join Now
Telegram Join Join Now
Download our app now हमारी app डाउनलोड करे

प्वॉइजली का सूत्र या नियम  (poiseuille’s equation in hindi)

By   October 23, 2018
0
(poiseuille’s equation in hindi) प्वॉइजली का सूत्र या नियम  : हम जानते है कि किसी पाइप में किसी द्रव के बहने का कारण दाब में अंतर होता है अर्थात जब दो बिन्दुओं या जगहों के मध्य दाब का अंतर होता है तो द्रव उच्च दब वाली जगह से निम्न दाब वाली जगह की तरफ बहता है।
दोनों बिन्दुओं या जगहों के मध्य दाब का अंतर जितना अधिक होगा , द्रव उतने ही अधिक वेग से बहता है।
माना किन्ही दो बिन्दुओं का दाब क्रमश: P1 तथा P2 है तथा इस दाब में अंतर के कारण तरल या द्रव Q दर से बहने लगता है तो इनके आपस के सम्बन्ध को निम्न सूत्र द्वारा प्रदर्शित करते है –

यहाँ P2 उच्च दाब बिंदु तथा P1 निम्न दाब बिंदु तथा Q = द्रव या तरल की प्रवाह दर , R = द्रव के प्रवाह के मार्ग में बाधा या प्रतिरोध का मान।
यहाँ ध्यान देने वाली बात यह है कि जिस द्रव या तरल की श्यानता का मान जितन अधिक होता है उसका प्रतिरोध उतना ही अधिक होता है जिससे अधिक श्यानता वाले द्रव का प्रवाह बहुत धीमी गति से होता है।
जिस नली का लम्बाई अधिक होती है उसका प्रतिरोध उतना ही अधिक होता है तथा जब किसी नली के अनुप्रस्थ क्षेत्रफल को बढाया जाता है तो इसका प्रतिरोध का मान कम हो जाता है क्यूंकि द्रव का प्रवाह आसानी से हो सकता है अर्थात द्रव के मार्ग में बाधा कम होती है।
किसी द्रव या तरल के लिए यदि श्यानता का मान शून्य होता है तो उस द्रव को घर्षणरहित तरल कहा जाता है और इसके लिए प्रतिरोध का मान शून्य होता है।
जब कोई द्रव किसी r त्रिज्या वाली नली से बह रहा है , नली की लम्बाई l है तथा द्रव की श्यानता का मान n है तो क्षैतिज में इस द्रव के रेखीय प्रवाह में उत्पन्न प्रतिरोध या बाधा का मान निम्न सूत्र द्वारा ज्ञात किया जाता है –

सब्सक्राइब करे youtube चैनल

इस समीकरण को द्रव के मार्ग में प्रतिरोध के लिए प्वॉइजली का समीकरण कहते है।

प्वॉइजली का नियम

यदि किसी द्रव का एक समान परिच्छेद वाली नली में रेखीय प्रवाह हो रहा है तो प्वॉइजली के अनुसार इस नली से द्रव का प्रति सेकंड प्रवाहित द्रव का आयतन निम्न बातों पर निर्भर करता है –
1. नली के दोनों सिरों के मध्य दाब (P) में अंतर के समानुपाती होता है।
2. नलिका के अनुप्रस्थ त्रिज्या (r) के चार घात के समानुपाती होता है।
3. द्रव या तरल की श्यानता (n) के मान के व्युत्क्रमानुपाती होता है।
4. नलिका की कुल लम्बाई (l) के भी व्युत्क्रमानुपाती होता है।

प्वॉइजली का सूत्र

प्वॉइजली ने अपने नियम में जो भी बिंदु बताये जब उनको आपस में रखा जाता है तो एक सूत्र का निर्माण होता है जिसकी सहायता से नली से द्रव का प्रति सेकंड प्रवाहित द्रव का आयतन का मान ज्ञात किया जा सकता है , यह सूत्र निम्न है –
यहाँ π/8 = K होता है जो एक नियतांक है जो समानुपाती का चिन्ह हटाने पर आया है इसलिए इसे समानुपाती नियतांक कहते है।
इस समीकरण को निम्न प्रकार भी लिखा जा सकता है –
द्रव के प्रवाह की दर V = p/R
यहाँ R = द्रव का प्रतिरोध है जिसका अध्ययन हम ऊपर कर चुके है।

हिंदी माध्यम नोट्स

Class 6

Hindi social science science maths English

Class 7

Hindi social science science maths English

Class 8

Hindi social science science maths English

Class 9

Hindi social science science Maths English

Class 10

Hindi Social science science Maths English

Class 11

Hindi sociology physics physical education maths english economics geography History

chemistry business studies biology accountancy political science

Class 12

Hindi physics physical education maths english economics

chemistry business studies biology accountancy Political science History sociology

Home science Geography

English medium Notes

Class 6

Hindi social science science maths English

Class 7

Hindi social science science maths English

Class 8

Hindi social science science maths English

Class 9

Hindi social science science Maths English

Class 10

Hindi Social science science Maths English

Class 11

Hindi physics physical education maths entrepreneurship english economics

chemistry business studies biology accountancy

Class 12

Hindi physics physical education maths entrepreneurship english economics

chemistry business studies biology accountancy