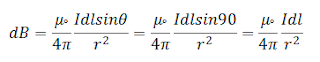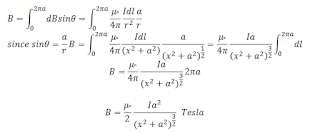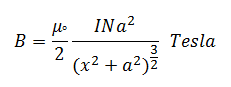Magnetic Field on the axis of current carrying circular coil in hindi वृत्ताकार धारावाही कुण्डली की अक्ष पर चुम्बकीय क्षेत्र
प्रस्तावना : हम पिछले टॉपिक में वृत्ताकार कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का अध्ययन कर चुके है और इसके सूत्र की स्थापना कर चुके है अब बात करते कुंडली के अक्ष पर चुंबकीय क्षेत्र कितना होगा और इसका सूत्र क्या होगा।
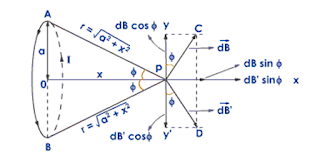
वृत्ताकार धारावाही कुंडली के अक्ष पर उत्पन्न चुम्बकीय क्षेत्र : माना a त्रिज्या की एक वृत्ताकार कुण्डली में I धारा प्रवाहित हो रही है। कुंडली में तार के N फेरे है। कुंडली के केंद्र O से x दूरी पर अक्षीय स्थिति में एक बिंदु P पर हमें चुम्बकीय क्षेत्र ज्ञात करना है। P पर कुंडली द्वारा अंतरित अर्द्ध शीर्ष कोण θ है। पहले हम एक लूप पर विचार करते है। माना लूप के व्यास NM के बिन्दुओ N और M पर समान लम्बाई dl के दो अल्पांश है। इन अल्पांशों की बिंदु P से दूरी यदि r हो तो N पर स्थित अल्पांश के कारण P पर उत्पन्न चुम्बकीय क्षेत्र
dB1 = (u0/4π)I.dl.sin90/r2
dB1 = (u0/4π)I.dl /r2
इसी प्रकार M पर स्थित समान लम्बाई के अल्पांश के कारण P पर उत्पन्न चुम्बकीय क्षेत्र
dB2 = (u0/4π)I.dl.sin90/r2
dB2 = (u0/4π)I.dl /r2
चित्र से स्पष्ट है कि केंद्र O के दोनों ओर सममित में लिए गए समान लम्बाई (dl) के दो अल्पांशों द्वारा बिंदु P पर समान परिमाण के चुम्बकीय क्षेत्र dB1 और dB2 उत्पन्न होते है। इन दोनों के निरक्षीय घटक dB1cosθऔर dB2cosθ परिमाण में समान और दिशा में विपरीत होने के कारण एक दुसरे को निष्प्रभावित कर देते है तथा अक्षीय घटक dB1sinθऔर dB2sinθ जुड़कर अक्षीय क्षेत्र प्रदान करते है। इस प्रकार अक्षीय क्षेत्र केवल अक्षीय घटक dBsinθ के कारण ही मिलता है।
चूँकि बिंदु P पर पूरी रिंग के कारण उत्पन्न चुम्बकीय क्षेत्र
B = u0.I.a2/2(a2 + x2)3/2
अत: कुण्डली में N फेरे है अत: कुंडली की अक्ष पर उसके केंद्र से x दूरी पर उत्पन्न चुम्बकीय क्षेत्र
B = u0.N.I.a2/2(a2 + x2)3/2
सामने से देखने पर यदि धारा वामावर्त दिशा में बहती हुई प्रतीत होती है तो उक्त क्षेत्र की दिशा कुंडली के तल के लम्बवत बाहर की तरफ होगी तथा यदि धारा दक्षिणावर्त दिशा में बहती हुई प्रतीत होती है तो उक्त क्षेत्र की दिशा कुंडली के तल के लम्बवत अन्दर की ओर होगी।
कुंडली के अक्षीय चुम्बकीय क्षेत्र का केंद्र O से दूरी के साथ परिवर्तन चित्र में दिखाया गया है।
B = u0.N.I.a2/2(a2 + x2)3/2 से स्पष्ट है कि
(i) जब x = 0 तो B = u0.N.I/2a
जो कि चुम्बकीय क्षेत्र का अधिकतम मान है अत: चुम्बकीय क्षेत्र का मान कुंडली के केंद्र पर अधिकतम होता है।
(ii) केंद्र O से बिंदु P की दूरी x बढ़ने पर B का मान घटता है।
(iii) जब x = ± ∞ तो B = 0 अर्थात अनंत पर B का मान शून्य हो जाता है।
(iv) दूरी के साथ चुम्बकीय क्षेत्र के परिवर्तन की दर अर्थात dB/dx सभी स्थानों पर एक समान नहीं होती है।
x = ± a/2 पर dB/dx का मान अधिकतम होता है।
प्रश्न : 10 सेंटीमीटर त्रिज्या की 100 कसकर लपेटे गये फेरों की किसी ऐसी कुण्डली पर विचार कीजिये जिसमें एक एम्पियर विद्युत धारा प्रवाहित हो रही है। कुंडली के केंद्र पर चुम्बकीय क्षेत्र का परिमाण क्या है ?
उत्तर : B = 6.28 x 10-4 T
प्रश्न : एक वृत्ताकार खण्ड की त्रिज्या 20 सेंटीमीटर है और यह अपने केंद्र पर 45 डिग्री का कोण बनाता है। यदि खंड में 10 एम्पियर की धारा प्रवाहित की जाए तो केंद्र पर उत्पन्न चुम्बकीय क्षेत्र का मान और दिशा ज्ञात कीजिये ?
उत्तर : चुंबकीय क्षेत्र B = 3.925 x 10-6 T
दिशा : चित्र के अनुसार वृत्तीय चाप में धारा दक्षिणावर्त है अत: केंद्र O पर चुम्बकीय क्षेत्र की दिशा खंड के तल के लम्बवत निचे की ओर होगी। यदि धारा की दिशा वामावर्त होती है तो चुम्बकीय क्षेत्र की दिशा खण्ड के तल के लम्बवत ऊपर की ओर होगी।