अनन्त लम्बाई के सीधे धारावाही चालक के कारण चुम्बकीय क्षेत्र Magnetic field due to infinite conductor
हमें इस अनन्त लम्बाई के तार में विद्युत धारा प्रवाहित होने पर तार से किसी दुरी पर स्थित किसी बिंदु पर चुम्बकीय क्षेत्र का मान ज्ञात करना है।
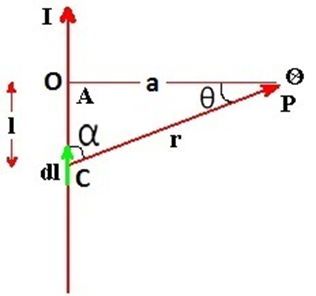
माना चित्रानुसार एक चालक तार है जिसमे I परिमाण की धारा प्रवाहित हो रही है , चालक तार से r दूरी पर कोई बिंदु P स्थित है , हमें इस बिंदु पर चुम्बकीय क्षेत्र का मान ज्ञात करना है।
जैसा की हम सब जानते है की इस चालक तार में विद्युत धारा प्रवाहित होने पर इसके चारों ओर संकेन्द्रिय वृतों के रूप में चुंबकीय क्षेत्र उत्पन्न हो जाता है इसलिए हम इस तार के चारों तरफ वृत्ताकार पथ की कल्पना करते है।
हम जो वृत्ताकार पथ की कल्पना कर रहे है इसकी त्रिज्या r मान रहे है।
एम्पीयर का नियम बताता है की
ऐम्पियर के नियम के उपयोग (application of ampere’s circuital law) :
(i) अनंत लम्बाई के सीधे धारावाही चालक तार के कारण चुम्बकीय क्षेत्र : माना XY एक लम्बा और सीधा धारावाही चालक है जिसमें I धारा बह रही है। तार से r दूरी पर स्थित बिंदु P पर चुम्बकीय क्षेत्र की तीव्रता ज्ञात करनी है। इसके लिए तार को केंद्र मानकर r त्रिज्या का एक बन्द वृत्तीय पथ खींच लेते है तो बिन्दु P इसी पथ पर पड़ेगा। पूरे पथ पर चुम्बकीय क्षेत्र का मान (परिमाण ) समान होगा तथा प्रत्येक बिन्दु पर चुम्बकीय क्षेत्र की दिशा पथ की स्पर्श रेखा की दिशा में होगी। इस प्रकार P पर B और अल्पांश dl एक ही दिशा में होगा।
एम्पियर के परिपथीय नियम से –
∮B.dl = μ0I . . . . . . . . समीकरण-1
या
∮B.dl.cos0 = μ0I
या
∮B.dl = μ0I
B.2πr = μ0I
B = μ0I/2πr
या
B = μ0.2I/4πr . . . . . . . . समीकरण-2
यही अनंत लम्बाई के धारावाही तार के कारण उत्पन्न चुम्बकीय क्षेत्र का व्यंजक है।
(ii) धारावाही परिनालिका के अन्दर उत्पन्न चुम्बकीय क्षेत्र : माना बेलनाकार ढाँचे पर लपेटी गयी एक लम्बी परिनालिका है। जब इसमें I धारा बहायी जाती है तो एक चुम्बकीय क्षेत्र उत्पन्न हो जाता है।
एक सीधी परिनालिका द्वारा उत्पन्न चुम्बकीय क्षेत्र एक दण्ड चुम्बक के द्वारा उत्पन्न चुम्बकीय क्षेत्र के समान होता है। परिनालिका के अन्दर चुम्बकीय क्षेत्र समरूप होता है तथा परिनालिका की अक्ष के अनुदिश होता है। माना परिनालिका के काफी अन्दर किसी बिंदु पर चुम्बकीय क्षेत्र B है।
B का मान ज्ञात करने के लिए ABCD एक आयताकार बंद पथ की कल्पना करते है। माना आयताकार पथ की लम्बाई AB = L है। स्वाभाविक है कि आयत द्वारा परिबद्ध फेरों की संख्या nL होगी , जहाँ n एकांक लम्बाई में फेरों की संख्या है। चूँकि धारा आयताकार बंद पथ को nL बार काटती है। अत: बन्द लूप से गुजरने वाली कुल धारा = nLI होगी।
एम्पियर के परिपथीय नियमानुसार , चुम्बकीय क्षेत्र B का रेखीय समाकलन आयताकार पथ ABCD के अनुदिश –
∮B.dl = μ0(nLI) . . . . . . . . समीकरण-3
चूँकि ABCD B.dl = A ∫BB.dl + B∫cB.dl + c∫DB.dl + D∫AB.dl . . . . . . . . समीकरण-4
चूँकि B की दिशा BC और AD के लम्बवत है , अत:
B∫cB.dl = D∫AB.dl = 0
ऐसी परिनालिका , जिसकी लम्बाई उसके व्यास की तुलना में काफी अधिक है , के कारण परिनालिका के बाहर बिन्दुओं पर चुम्बकीय क्षेत्र शून्य होता है।
अत: c∫DB.dl = 0
अत: समीकरण-4 से –
ABCD∮B.dl = A∫B B.dl = A∫B B.dl.cos0 = B A∫B dl
अत: A∫B dl = L = आयताकार पथ ABCD की भुजा AB की लम्बाई
अत: ABCD∮B.dl = BL . . . . . . . . समीकरण-5
समीकरण-3 का उपयोग करने पर –
μ0.nLI = BL
अत: B = μ0.nI
यह चुम्बकीय क्षेत्र एक लम्बी परिनालिका के अन्दर उसकी अक्ष लगभग केंद्र पर होता है अर्थात
Bc = μ0.nI . . . . . . . . समीकरण-6
प्रयोगो से यह पाया गया कि लम्बी परिनालिका के किनारों पर उत्पन्न क्षेत्र उसके केंद्र पर उत्पन्न चुम्बकीय क्षेत्र का आधा होता है। अत: परिनालिका के किनारे उत्पन्न चुम्बकीय क्षेत्र
Be = μ0.nI/2 . . . . . . . . समीकरण-7
यदि परिनालिका काफी लम्बी है तो इसके सिरों के पास के स्थानों को छोड़कर परिनालिका के भीतर सभी बिन्दुओं पर चुम्बकीय क्षेत्र एक समान होता है। चुम्बकीय क्षेत्र का मान परिनालिका की लम्बाई और परिच्छेद के क्षेत्रफल पर निर्भर नहीं करता है। इस प्रकार धारावाही परिनालिका एक ज्ञात और एकसमान चुम्बकीय क्षेत्र उत्पन्न करने का साधन है। चुम्बकीय क्षेत्र की दिशा परिनालिका के अक्ष के अनुदिश होती है।
परिनालिका के अन्दर चुम्बकीय क्षेत्र B का परिवर्तन दूरी x के साथ चित्र में दिखाया गया है।
यदि परिनालिका की लम्बाई l हो तथा उसमें फेरो की संख्या N हो तो
n = N/l . . . . . . . . समीकरण-8
अत: समीकरण-6 को निम्नलिखित प्रकार व्यक्त कर सकते है –
Bc = μ0.NI/l . . . . . . . . समीकरण-9
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics