Lorentz Transformation in hindi equations लोरेंत्ज़ परिवर्तन समीकरण क्या है , लॉरेन्ज रूपान्तरण किसे कहते हैं

यहाँ जान पाएंगे कि Lorentz Transformation in hindi equations लोरेंत्ज़ परिवर्तन समीकरण क्या है , लॉरेन्ज रूपान्तरण किसे कहते हैं ?

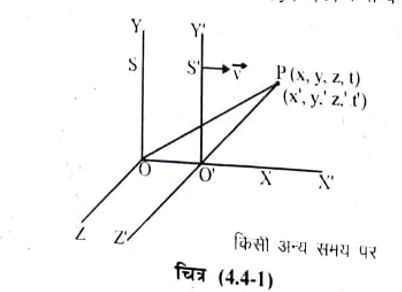
लॉरेन्ज रूपान्तरण (Lorentz Transformations) : माना S और S’ दो जडत्वीय निर्देश तन्त्र हैं | निर्देश तन्त्र S’ नियत वेग v से तंत्र S के सापेक्ष +X दिशा में इस प्रकार गति कर रहा है कि दोनों तन्त्रों के Y और Z अक्ष परस्पर समान्तर रहे जैसा कि चित्र में दर्शाया है |

दोनों निर्देश तन्त्रों के मूल बिन्दुओं क्रमशः O और O’ पर स्थित प्रेक्षकों के लिए t और t’ किसी घटना के प्रेक्षित समय है | सुविधा की दृष्टि से हम मानते है कि जब दोनों प्रेक्षकों की घड़ियाँ शून्य समय बताती है अर्थात t = t’ = 0 पर दोनों तंत्रों के मूल बिंदु O और O’ सम्पाती होते है | मान लीजिये किसी बिंदु के निर्देशांक निर्देश तन्त्र S और S’ में क्रमशः (x,y,z) और (x’,y’,z’) है | लोरेन्ज रुपान्तरण से (x,y,z,t) और (x’,y’,z’,t’) में सम्बन्ध स्थापित करते हैं |

अब कल्पना करते है कि t = t’ = 0 पर मूल बिंदु O और O’ से जो इस क्षण संपाती है एक क्षण दीप्ती (फ्लेश) उत्सर्जित होती है जिससे आकाश में O के चारों तरफ एक गोलाकार तरंगाग्र (spherical wavefront) वेग c (प्रकाश का वेग) से फैलता है | आपेक्षिकता के प्रथम अभिगृहीत के अनुसार तन्त्र S’ के सापेक्ष भी यह स्पंदन O’ के चारों तरफ समान वेग c से गोलाकार तरंगाग्र के रूप में प्रगति करता हुआ प्रतीत होगा |

अत: यदि प्रेक्षक O द्वारा गोलीय तरंगाग्र को किसी बिंदु P , जिसके स्थिति निर्देशांक S तन्त्र में (x,y,z) है , पर पहुँचने में लगा समय t नापा जाता है तो

t = OP/c = (x² + y² + z²)^1/2 /c

अथवा

x² + y² + z² – c²t² = 0

इसी प्रकार यदि प्रेक्षक O’ गोलीय तरंगाग्र को बिंदु P पर पहुँचाने में लगा समय t’ नापता है तो S’ तन्त्र में क्षण दीप्ती को P पर पहुँचने पर लगा समय

t = O’P/c = (x’² + y’² + z’²)^1/2/c

अथवा

x’² + y’² + z’² – c²t’² = 0

यहाँ (x’,y’,z’) तन्त्र S’ में बिंदु P के स्थिति निर्देशांक हैं |

चूँकि एक ही बिंदु P के लिए समीकरण (1) और (2) वैध है इसलिए समीकरण (1) और (2) का परस्पर रुपान्तरण एक निर्देश तन्त्र से दुसरे निर्देश तन्त्र में हो जाना चाहिए | इसलिए सभी जडत्वीय निर्देश तंत्रों में x² + y² + z² – c²t² का मान अचर होना चाहिए अर्थात एक ही घटना (इवेंट) के लिए S तन्त्र में निर्देशांक (x,y,z,t) और S’ तन्त्र में निर्देशांक (x’,y’,z’,t’) में रूपान्तरण इस प्रकार होने चाहिए कि समीकरण (1) और (2) सदैव वैध रहे |

जैसा हम जानते हैं कि निम्न गैलीलियन रूपान्तरण सभी जडत्वीय निर्देश तन्त्रों के निर्देशांकों के संबंध को व्यक्त करता है :

x’ = x – vt , y’ = y , z’ = z और t’ = t

सर्वप्रथम गैलीलियन रुपान्तरण की वैधता को उपरोक्त प्रकार के निकाय के लिए ज्ञात करेंगे |

समीकरण -3 को समीकरण-2 में रखने पर ,

(x-vt)² + y² + z² – c²t² = 0

अथवा

x² + (-2x vt + v²t²) + y² + z² – c²t² = 0

उपरोक्त समीकरण (-2xvt + v²t²) अतिरिक्त पद के कारण समीकरण (1) के समतुल्य नहीं आता है | इसलिए इस प्रकार के निर्देश तन्त्र जिसमें प्रकाश का वेग अचर माना जाता है , गैलीलियन रूपान्तरण समीकरण 3 वैध नहीं रहते है लेकिन समीकरण 1 और समीकरण 4 की तुलना करने से यह ज्ञात होता है कि y’ = y और z’ = z होता है | समीकरण (4) में अतिरिक्त पद (-2xvt + v²t²) यह व्यक्त करता है कि x और t के रुपान्तरण इस प्रकार होने चाहिए कि अतिरिक्त पद समीकरण में विलुप्त हो जाए | अत: मान लीजिये समान घटना के लिए रैखिक (लीनियर) रुपान्तरण समीकरण निम्नलिखित है :

x’ = (αx + βt) , y’ = y  , z’ = z और t’ = (γx + δt)

(चूँकि S’ की गति X दिशा में है अत: y और z निर्देशांक अपरिवर्तित रहेंगे)

यहाँ α , β , γ और δ नियतांक है जिनका मान ज्ञात करना है |

चूँकि हम जानते है कि निर्देश तन्त्र S के सापेक्ष प्रेक्षक O’ (जिसके लिए x’ = 0) + X अक्ष के अनुदिश v वेग से गति कर रहा है | अत: x’ = 0 पर स्थित प्रेक्षक O’ का S के सापेक्ष वेग dx/dt = v होगा |

x’ = 0 रखने पर समीकरण x’ = (αx + βt) से

0 = (αx + βt)

अथवा dx/dt = -β/α = v

अथवा β = -αv

इसी प्रकार निर्देश तंत्र S’ के सापेक्ष O (जिसके लिए x = 0 है) -X अक्ष के अनुदिश -v वेग से गति करता हुआ दिखाई देता है | इसलिए x = 0 पर प्रेक्षक O का वेग

= dx’/dt’ = -v

समीकरण t’ =  γx + δt और x’ = αx + βt में उपरोक्त मान रखने पर t’ = δt और x’ = βt

जिससे x’ = βt’/δ  = αvt’/δ

और dx’/dt’ = αv/δ = -v (समीकरण 7 से)

अत: α = δ

β और δ के मानों को समीकरण 5 में रखने पर रुपान्तरण समीकरण निम्न हो जायेंगे –

x’ = α(x-vt)

y’ = y

z’ = z

t’ = γx + αt

अब समीकरण 9 को समीकरण 2 में रखने पर –

α²(x-vt)² + y² + z² – c² (γx + αt)² = 0

अथवा (α² – c²γ²)x² + (-2 α²v – 2c² γ α)xt + y² + z² – t²(-α²v² + c² α²) = 0

इस समीकरण की तुलना समीकरण (1) से करने पर –

α² – c²γ² = 1

-2 α²v – 2c² α γ = 0

– α²v² + α²c² = c²

समीकरण (12) से ,

α = c/ √c²-v²   = 1/ √1-v²/c²

इसी प्रकार समीकरण 11 से –

-2 α²v – 2c² α γ = 0

अथवा γ = – αv/c²

समीकरण 13 और समीकरण 14 को समीकरण 9 में रखने पर

आपेक्षिकता के विशिष्ट सिद्धांत के अनुरूप रूपान्तरण समीकरण होंगे |

x’ = α(x-vt)

y’ = y

z’ = z

t’ = α(t-vx/c²)

जहाँ α = 1/√1-v²/c²

समीकरण 15 लोरेन्ज रूपान्तरण समीकरण कहलाते है |

यदि S’ निर्देश तन्त्र का वेग v प्रकाश के वेग c के सापेक्ष नगण्य हो तो

अर्थात v/c <<1 तो  α = 1

इस परिस्थिति में

समीकरण 15 गैलीलियन रुपान्तरण समीकरण में परिवर्तित हो जाते है |

अर्थात

x’ = (x-vt)

y’ = y

z’ = z

t’ = t

आपेक्षिकता के विशिष्ट सिद्धांत के अनुसार निर्देश तन्त्र S’ के सापेक्ष निर्देश तन्त्र S नियत वेग -v से गति करता हुआ माना जा सकता है | अत: प्रतिलोम लोरेन्ज रूपान्तरण v को -v से प्रतिस्थापित करके ज्ञात कर सकते है | अत: S’ निर्देश तन्त्र के सापेक्ष S तन्त्र में रुपान्तरण समीकरण होंगे –

x = α(x’ + vt’)

y = y’

z = z’

t = α(t’ + vx’/c²)

स्पष्टत: लॉरेन्ज समीकरण रैखिक समीकरण (linear equations) होते हैं |