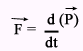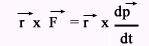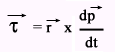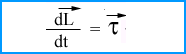कोणीय संवेग का संरक्षण का नियम या सिद्धांत (law of conservation of angular momentum in hindi)
(law of conservation of angular momentum in hindi) कोणीय संवेग का संरक्षण का नियम या सिद्धांत : जब किसी निकाय पर इसकी अक्ष पर कार्यरत कुल बाह्य बल आघूर्ण का मान शून्य हो तो उस अक्ष पर कुल कोणीय संवेग का मान नियत रखता है अर्थात संरक्षित रहता है , इसे ही कोणीय संवेग का नियम कहते है।
कोणीय संवेग के संरक्षण के नियम या सिद्धान्त का प्रमाण
कोणीय संवेग संरक्षण (conservation of angular momentum) : यदि कुल बलाघूर्ण Text = 0 तब dLz/dt = Text = 0 या Lz = नियत
या
Iw = नियत
या
Iiwi = Ifwg
अत: कोणीय संवेग संरक्षण के नियम की निम्नानुसार व्याख्या की जा सकती है –
‘यदि दृढ वस्तु या निकाय पर क्रियाशील कुल बाह्य बलाघूर्ण शून्य होता है , तब दृढ वस्तु या दृढ निकाय का कुल कोणीय संवेग नियत रहता है। इसे कोई भी फर्क नहीं पड़ता है कि निकाय में किस प्रकार का परिवर्तन किया गया है। ‘
नोट :
- ऊर्जा संरक्षण और रेखीय संवेग संरक्षण के समान , कोणीय संवेग संरक्षण का सिद्धान्त भी सार्वत्रिक संरक्षण नियम है जो कि परमाणवीय तथा नाभिकीय निकाय से गैलेक्सियो की गति तक वैध होता है। यह उन कणों के लिए वैध होता है , जिनकी चालें प्रकाश की चाल के निकट होती है , जहाँ न्यूटन यांत्रिकी असफल होती है। इसके लिए कोई भी अपवाद कभी भी नहीं पाया गया है।
- केन्द्रीय बलों (दो बिंदु द्रव्यमानों के मध्य गुरुत्वीय बल तथा दो बिंदु आवेशो के मध्य कुलाम बल के समान ) के कारण , कुल बलाघूर्ण Text = 0 होता है तथा इसलिए कोणीय संवेग संरक्षित रहता है।
- आंतरिक बल , निकाय के भाग का कोणीय संवेग परिवर्तित कर सकते है लेकिन कुल कोणीय संवेग परिवर्तित नहीं कर सकते है।
- सामान्यतया सम्बन्ध Text = dL/dt जडत्वीय तंत्र में सत्य होता है। फिर भी , अजडत्वीय होने के बावजूद यह द्रव्यमान केंद्र तंत्र में भी सही है।
कोणीय संवेग संरक्षण पर आधारित कुछ उदाहरण
यहाँ τ और L समान अक्ष के सापेक्ष है।
यदि किसी कण अथवा निकाय पर τबाह्य = 0 हो तो कण अथवा निकाय का कोणीय संवेग , उस बिंदु या घूर्णन अक्ष के सापेक्ष नियत रहता है।
बलाघूर्ण का आवेग : ∫τdt = △J
△J = कोणीय संवेग में परिवर्तन
(1) मान लो हम किसी लम्ब धागे के एक सिरे पर गेंद बाँधकर धागे के दुसरे सिरे को एक उधर्व नली में से गुजारकर हाथ में पकड़ लेते है , और दुसरे हाथ से नली को पकड़कर गेंद को क्षैतिज वृत्त में घुमा रहे है , यदि हम धागे को नीचे की ओर खींचकर गेंद के वृत्तीय पथ की त्रिज्या को छोटा कर दे तो गेंद पहले से अधिक तेजी से घुमने लगती है। इसका कारण यह है कि वृत्त की त्रिज्या घटने से गेंद का घूर्णन अक्ष के परित: जडत्व आघूर्ण घट जाता है अत: संवेग संरक्षण के नियमानुसार , गेंद का कोणीय वेग बढ़ जाता है।
(2) जब कोई तैराक ऊपर से जल में कूदता है तो वह सीधे कूदने के बजाय , अपने शरीर को मोड़ लेता है। इससे उसके शरीर का जड़त्व आघूर्ण I घट जाता है लेकिन Iw का मान नियत रहता है अत: I के घटने से कोणीय वेग w बढ़ जाता है। अब वह कूद के दौरान वायु में कलैया ले लेता है।
(3) एक व्यक्ति अपनी भुजाओ को फैलाकर अपने हाथो में भारी डम्बल लिए एक घूमते हुए स्टूल पर खड़ा है। जब वह व्यक्ति अपनी भुजाओ को समेट लेता है तो तुरंत स्टूल की गति तेज हो जाती है। कारण यह है कि भुजाओं को समेट लेने पर डम्बलों की घूर्णन अक्ष से दूरी R घट जाती है जिससे व्यक्ति का जडत्व आघूर्ण कम हो जाता है अत: कोणीय वेग बढ़ जाता है। भुजाओं को पुनः फैला देने पर स्टूल की गति पुनः धीमी हो जाती है। इसी प्रकार बर्फ पर स्केटिंग करने वाले अपनी भुजाओ को फैलाकर और मोड़कर स्केटिंग की गति बदलते है।
प्रश्न : m द्रव्यमान और l लम्बाई की समरूप छड H बिंदु पर किलकित है। यह क्षैतिज तल में उर्ध्वाधर अक्ष के सापेक्ष मुक्त रूप से घूर्णन कर सकती है। समान द्रव्यमान m का एक बिंदु द्रव्यमान प्रारंभिक वेग u से छड के लम्बवत गति करता हुआ , छड के मुक्त सिरे से पूर्णतया अप्रत्यास्थ टक्कर (e = 0 ) करता है तो टक्कर के तुरंत बाद छड का कोणीय वेग ज्ञात करो ?
हल : चूँकि क्षैतिज तल में कोई बाह्य बल उपस्थित नहीं है इसलिए कोणीय संवेग नियत रहता है। यह क्षैतिज तल में H के सापेक्ष बल आघूर्ण उत्पन्न करता है।
mul = (ml2/3 + ml2)w
w = 3a/4l
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics