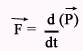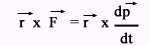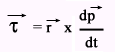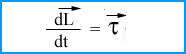WhatsApp Group Join Now

Telegram Join Join Now

कोणीय संवेग का संरक्षण का नियम या सिद्धांत (law of conservation of angular momentum in hindi)

SbistudyNovember 7, 2018inphysics

(law of conservation of angular momentum in hindi) कोणीय संवेग का संरक्षण का नियम या सिद्धांत : जब किसी निकाय पर इसकी अक्ष पर कार्यरत कुल बाह्य बल आघूर्ण का मान शून्य हो तो उस अक्ष पर कुल कोणीय संवेग का मान नियत रखता है अर्थात संरक्षित रहता है , इसे ही कोणीय संवेग का नियम कहते है।

अत: कोणीय संवेग सिद्धांत के अनुसार निम्न सम्बन्ध पाया जाता है –

कोणीय संवेग के संरक्षण के नियम या सिद्धान्त का प्रमाण

जैसा कि हमने गति के द्वितीय नियम में पढ़ा था कि किसी वस्तु पर कार्यरत कुल बल का मान वस्तु में रेखीय संवेग में परिवर्तन की दर के बराबर होता है।

अत:

दोनों तरफ r का गुणा करने पर

चूँकि हम जानते है की r x F = वस्तु पर कार्यरत बल आघूर्ण होता है जिसे T से व्यक्त करते है , अत: यह समीकरण निम्न प्रकार आता है –

चूँकि r x p = वस्तु का कोणीय संवेग L के बराबर होता है।

अत:

यह समीकरण दर्शाती है किसी कण पर कार्य कर रहे बल आघूर्ण का मान कोणीय संवेग में परिवर्तन की दर के बराबर होता है।

यदि कण पर कार्यरत बलाघूर्ण का मान शून्य हो तो

दोनों तरफ समाकलन करने पर

अत: हम देख सकते है जब किसी कण पर कार्यरत बल आघूर्ण का मान शून्य हो तो कण के कोणीय संवेग का मान नियत या संरक्षित रहता है जैसा हम समीकरण में भी देख सकते है , इसे ही संवेग संरक्षण का नियम या सिद्धांत कहते है।

कोणीय संवेग से

L = I x w

अत: कोणीय संरक्षण के नियम से

L = I x w = नियत

I ∝ 1/w

अत: हम कह सकते है कि जब किसी वस्तु पर कार्यरत बल आघूर्ण का मान शून्य हो तो इस स्थिति में वस्तु का जडत्व आघूर्ण I , वस्तु के कोणीय वेग के व्युत्क्रमानुपाती होता है।

अर्थात जड़त्व आघूर्ण का मान बढाने पर , कोणीय वेग का मान कम हो होगा तथा जड़त्व आघूर्ण का मान कम होने पर कोणीय वेग अधिक होगा।

उदाहरण : सूर्य के चारों तरफ दीर्घवृत्ताकार कक्षा में जब ग्रह चक्कर लगाता रहता है तो जब ग्रह सूर्य के पास से गुजरता है तो ग्रह का जड़त्व आघूर्ण का मान कम हो जाता है जिसके कारण ग्रह की परिक्रमण गति बढ़ जाती है और सूर्य से ग्रह की दूरी अधिक होने पर उसका जडत्व आघूर्ण अधिक हो जाता है जिससे ग्रह का कोणीय वेग का मान कम हो जाता है , यहाँ कोणीय संवेग संरक्षण का नियम या सिद्धांत लागू होता है।

कोणीय संवेग संरक्षण (conservation of angular momentum) : यदि कुल बलाघूर्ण T_ext = 0 तब dL_z/dt = T_ext = 0 या L_z = नियत

या

I_w = नियत

या

I_iw_i = I_fw_g

अत: कोणीय संवेग संरक्षण के नियम की निम्नानुसार व्याख्या की जा सकती है –

‘यदि दृढ वस्तु या निकाय पर क्रियाशील कुल बाह्य बलाघूर्ण शून्य होता है , तब दृढ वस्तु या दृढ निकाय का कुल कोणीय संवेग नियत रहता है। इसे कोई भी फर्क नहीं पड़ता है कि निकाय में किस प्रकार का परिवर्तन किया गया है। ‘

नोट :

ऊर्जा संरक्षण और रेखीय संवेग संरक्षण के समान , कोणीय संवेग संरक्षण का सिद्धान्त भी सार्वत्रिक संरक्षण नियम है जो कि परमाणवीय तथा नाभिकीय निकाय से गैलेक्सियो की गति तक वैध होता है। यह उन कणों के लिए वैध होता है , जिनकी चालें प्रकाश की चाल के निकट होती है , जहाँ न्यूटन यांत्रिकी असफल होती है। इसके लिए कोई भी अपवाद कभी भी नहीं पाया गया है।
केन्द्रीय बलों (दो बिंदु द्रव्यमानों के मध्य गुरुत्वीय बल तथा दो बिंदु आवेशो के मध्य कुलाम बल के समान ) के कारण , कुल बलाघूर्ण T_ext = 0 होता है तथा इसलिए कोणीय संवेग संरक्षित रहता है।
आंतरिक बल , निकाय के भाग का कोणीय संवेग परिवर्तित कर सकते है लेकिन कुल कोणीय संवेग परिवर्तित नहीं कर सकते है।
सामान्यतया सम्बन्ध T_ext = dL/dt जडत्वीय तंत्र में सत्य होता है। फिर भी , अजडत्वीय होने के बावजूद यह द्रव्यमान केंद्र तंत्र में भी सही है।

कोणीय संवेग संरक्षण पर आधारित कुछ उदाहरण

1. जब एक गोताखोर किसी ऊँचाई से जल में कूदता है , तब वह अपने शरीर को सीधा नहीं रखता है बल्कि शरीर के केन्द्र की ओर अपनी भुजाओं तथा पैरों को खींचता है ताकि उसके शरीर का जड़त्व आघूर्ण (I) घट जाए | चूँकि शरीर पर कोई बाह्य बलाघूर्ण क्रियाशील नहीं है अत: कोणीय संवेग (Iw) नियत रहता है एवं इसलिए जब I घटता है , तब कोणीय वेग (w) बढ़ता है इसलिए कूदते समय हम वायु में अपने शरीर को घुमा सकते है |

2. एक गेंद को रस्सी के एक सिरे से बांधा गया है , जिसका अन्य सिरा उर्ध्वाधर खोखली नली से गुजरता है | एक हाथ से नली को पकड़ा जाता है और दुसरे हाथ से रस्सी को पकड़ा जाता है | गेंद को क्षैतिज वृत्त में घूर्णन अवस्था में लाया जाता है |

यदि गेंद के वृत्ताकार पथ की त्रिज्या को छोटा कर रस्सी को नीचे की ओर खिंचा जाता है , तब गेंद पहले की अपेक्षा तेजी से घुमती है | इसका कारण यह है कि वृत्त की त्रिज्या को छोटा करने पर घूर्णन के अक्ष के सापेक्ष गेंद का जडत्व आघूर्ण घटता है इसलिए कोणीय संवेग के संरक्षण के नियम (Iw = नियत) के अनुसार , घूर्णन का कोणीय वेग बढ़ता है |

3. एक व्यक्ति अपनी भुजाओं को फैलाए और अपने प्रत्येक हाथ में भारी डम्बल की पकड़कर घुर्णिका के केंद्र पर खड़ा है | जब वह अपनी भुजाओं को खींचता है , तब इसके द्रव्यमान केंद्र से गुजरते उर्ध्वाधर अक्ष के सापेक्ष इसका जडत्व आघूर्ण घटता है और इसलिए कोणीय संवेग के संरक्षण के नियम से इसका कोणीय वेग बढ़ता है |

4. w₁ और w₂ कोणीय वेग से घूर्णन करती है और I₁ , I₂ जड़त्व आघूर्ण वाली पारगमन शाफ्ट संचरण स्तम्भ से जुडी दो चकतियो को दर्शाता है | जब हम इन्हें एक दूसरे की ओर धक्का देते है , तब चकतियों एक दूसरे से रगडती है और अनंत: कोणीय संवेग के संरक्षण से w = (I₁w₁ + I₂w₂/I₁ + I₂) उभयनिष्ठ कोणीय वेग प्राप्त करती है |

5. उपचक्र वाले वायुयान की स्थिति में अन्तरिक्ष में वायुयान की स्थिति उपचक्र के घूर्णन द्वारा परिवर्तित होती है | यदि उपचक्र एक दिशा में चक्रण करना प्रारंभ करता है , तब वायुयान कोणीय संवेग के संरक्षण से विपरीत दिशा में घूर्णन करेगा |

कोणीय संवेग संरक्षण :घूर्णन में न्यूटन का द्वितीय नियम : τ = dL/dt

यहाँ τ और L समान अक्ष के सापेक्ष है।

यदि किसी कण अथवा निकाय पर τ_{बाह्य} = 0 हो तो कण अथवा निकाय का कोणीय संवेग , उस बिंदु या घूर्णन अक्ष के सापेक्ष नियत रहता है।

बलाघूर्ण का आवेग : ∫τdt = △J

△J = कोणीय संवेग में परिवर्तन

(1) मान लो हम किसी लम्ब धागे के एक सिरे पर गेंद बाँधकर धागे के दुसरे सिरे को एक उधर्व नली में से गुजारकर हाथ में पकड़ लेते है , और दुसरे हाथ से नली को पकड़कर गेंद को क्षैतिज वृत्त में घुमा रहे है , यदि हम धागे को नीचे की ओर खींचकर गेंद के वृत्तीय पथ की त्रिज्या को छोटा कर दे तो गेंद पहले से अधिक तेजी से घुमने लगती है। इसका कारण यह है कि वृत्त की त्रिज्या घटने से गेंद का घूर्णन अक्ष के परित: जडत्व आघूर्ण घट जाता है अत: संवेग संरक्षण के नियमानुसार , गेंद का कोणीय वेग बढ़ जाता है।

(2) जब कोई तैराक ऊपर से जल में कूदता है तो वह सीधे कूदने के बजाय , अपने शरीर को मोड़ लेता है। इससे उसके शरीर का जड़त्व आघूर्ण I घट जाता है लेकिन Iw का मान नियत रहता है अत: I के घटने से कोणीय वेग w बढ़ जाता है। अब वह कूद के दौरान वायु में कलैया ले लेता है।

(3) एक व्यक्ति अपनी भुजाओ को फैलाकर अपने हाथो में भारी डम्बल लिए एक घूमते हुए स्टूल पर खड़ा है। जब वह व्यक्ति अपनी भुजाओ को समेट लेता है तो तुरंत स्टूल की गति तेज हो जाती है। कारण यह है कि भुजाओं को समेट लेने पर डम्बलों की घूर्णन अक्ष से दूरी R घट जाती है जिससे व्यक्ति का जडत्व आघूर्ण कम हो जाता है अत: कोणीय वेग बढ़ जाता है। भुजाओं को पुनः फैला देने पर स्टूल की गति पुनः धीमी हो जाती है। इसी प्रकार बर्फ पर स्केटिंग करने वाले अपनी भुजाओ को फैलाकर और मोड़कर स्केटिंग की गति बदलते है।

प्रश्न : m द्रव्यमान और l लम्बाई की समरूप छड H बिंदु पर किलकित है। यह क्षैतिज तल में उर्ध्वाधर अक्ष के सापेक्ष मुक्त रूप से घूर्णन कर सकती है। समान द्रव्यमान m का एक बिंदु द्रव्यमान प्रारंभिक वेग u से छड के लम्बवत गति करता हुआ , छड के मुक्त सिरे से पूर्णतया अप्रत्यास्थ टक्कर (e = 0 ) करता है तो टक्कर के तुरंत बाद छड का कोणीय वेग ज्ञात करो ?

हल : चूँकि क्षैतिज तल में कोई बाह्य बल उपस्थित नहीं है इसलिए कोणीय संवेग नियत रहता है। यह क्षैतिज तल में H के सापेक्ष बल आघूर्ण उत्पन्न करता है।

mul = (ml²/3 + ml²)w

w = 3a/4l