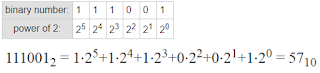दशमलव एवं द्विआधारीय संख्या पद्धतियाँ , बाइनरी सिस्टम (decimal and binary number system in hindi)
दशमलव संख्या पद्धति (decimal number system) : इस पद्धति का आधार दस (10) होता है , इस पद्धति में 1 से लेकर 10 तक अर्थात दस अंक होते है जो निम्न है – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
इस पद्धति के अंतर संख्या की स्थिति बहुत ही महत्वपूर्ण होती है , इसमें पहली स्थिति में शून्य फिर बायीं तरफ चलने पर स्थिति दस , सौ , हजार इस प्रकार से बढती जाती है।
इस पद्धति में डॉट भी लगा होता है जो दशमलव को दर्शाता है , दशमलव के दाई ओर 10−1 , 10−2 आदि होती है।
उदाहरण : 543.21 को दशमलव पद्धति संख्या पद्धति में प्रदर्शित कीजिये
543.21 को (5 × 102) + (4 × 101) + (3 × 100) + (2 × 10−1) + (1 × 10−2) लिखा जाता है , यहाँ हम देख सकते है कि हमने आधार दस लिया है और दशमलव के बाद आधार ऋणात्मक रूप में बढ़ता है जबकि दशमलव के बायीं तरफ दस का आधार 0 से चलता है और बढ़ता जाता है , इसी पद्धति को दशमलव संख्या पद्धति कहते है।
द्विआधारीय संख्या पद्धति (binary number system) (बाइनरी सिस्टम)
दशमलव पद्धति से द्विआधारीय संख्या पद्धति में परिवर्तन (decimal to binary number system)
- सबसे पहले संख्या को 2 से विभाजित करे।
- संख्या को दो से विभाजित करने के बाद जो भागफल प्राप्त होता है , उस भागफल को पुन: दो से विभाजित करे।
- शेषफल जो प्राप्त होता है वह द्विआधारीय संख्या होती है।
- स्टेप को बार बार तब तक दोहरायें जब तक की शेषफल शून्य प्राप्त न हो जाए।
- शेषफल को यदि उलटे क्रम में लिखा जाए तो परिवर्तित बाइनरी संख्या प्राप्त होती है।
बाइनरी (द्विआधारीय) संख्या को दशमलव संख्या में परिवर्तित करना (binary to decimal number conversion)
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics