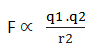कूलाम नियम क्या है , कूलॉम का नियम , coulomb’s law in hindi , सूत्र स्थापना या व्युत्पन्न , महत्व
coulomb’s law in hindi , सूत्र स्थापना या व्युत्पन्न , महत्व , कूलाम नियम क्या है , कूलॉम का नियम , कुलाम का नियम किसे कहते है , सूत्र स्थापना , विमा :-
परिभाषा : सन 1785 में प्रसिद्ध फ्रांसीसी वैज्ञानिक कूलॉम ने आवेशित वस्तुओं या दो बिंदु आवेशों के मध्य लगने वाले आकर्षण या प्रतिकर्षण के सन्दर्भ में एक नियम दिया जिसे कूलॉम का नियम कहते है।
कूलॉम के नियम का गणितीय निरूपण :
समानुपाती चिन्ह हटाने पर
यहाँ k = समानुपाती नियतांक कहते है।
k का मान आवेशों के मध्य उपस्थित माध्यम की प्रकृति और मात्रक पर निर्भर करता है।
शर्तें :
1. यदि आवेश निर्वात (वायु) में रखे है और बल न्यूटन (मात्रक ) में तथा दूरी (r) मीटर में है तथा आवेश कूलॉम में दिए गए है तो k (समानुपातिक नियतांक) का निम्न प्रकार प्रदर्शित किया जाता है।
k = K = 9 x 109
यहाँ ε0 (एप्साइलन जीरो ) को निर्वात की विद्युतशीलता कहते है।
निर्वात (वायु) में आवेशों के मध्य लगने वाला बल F0 है तो निम्न प्रकार से व्यक्त करते है।
2. यदि दो आवेश निर्वात (वायु) के अतिरिक्त अन्य किसी माध्यम में रखे है तो
यहाँ ε = माध्यम की विधुतशीलता कहलाता है।
अतः लगने वाला बल
कूलाम का नियम : फ़्रांसिसी वैज्ञानिक कूलॉम ने सन 1785 में आवेशित वस्तुओं के बीच कार्य करने वाले आकर्षण एवं प्रतिकर्षण बलों का परिमाणात्मक अध्ययन एंठन तुला के प्रयोग द्वारा किया और इस प्रयोग से प्राप्त प्रेक्षणों के आधार पर एक नियम की स्थापना की जिसे कूलॉम का व्युत्क्रम वर्ग नियम कहते है।
कूलॉम के नियम के अनुसार “दो स्थिर बिंदु आवेशों के मध्य कार्य करने वाले आकर्षण या प्रतिकर्षण बल दोनों आवेशों की मात्राओं के गुणनफल के अनुक्रमानुपाती और उनके मध्य की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह बल दोनों आवेशो को मिलाने वाली रेखा के अनुदिश होता है। ”
इस प्रकार यदि बिंदु आवेशो q1 व q2 के मध्य की दूरी r हो तो कूलाम के नियम के अनुसार उनके मध्य लगने वाला आकर्षण या प्रतिकर्षण बल
F ∝ q1q2
तथा F ∝ 1/r2
अत: F ∝ q1q2/r2
F = k q1q2/r2
यहाँ k समानुपातिक नियतांक है।
- जब दोनों आवेशों को कुलाम में व्यक्त किया जाए और दोनों आवेश निर्वात या वायु में रखे हो व बल को न्यूटन में , दूरी को मीटर में व्यक्त किया जाए तो k = 1/4πε0= 9 x 109 न्यूटन.मीटर2/कूलाम2
यहाँ एप्साइलन जीरो (ε0 ) , निर्वात की विद्युतशीलता है।
जब निर्वात अथवा वायु में आवेशों के मध्य लगने वाला बल F0 से व्यक्त करे तो कुलाम के नियमानुसार –
F0 = (1/4πε0) (q1q2/r2) न्यूटन
- यदि आवेश किसी अन्य माध्यम में रखे हो तो –
k = 1/4πε
यहाँ ε , माध्यम की विद्युतशीलता है।
अत: कुलाम के नियमानुसार –
F = (1/4πε) (q1q2/r2) न्यूटन
प्रयोगों से यह देखा गया कि दो बिंदु आवेशों के मध्य किसी निश्चित दूरी के लिए कार्य करने वाला बल निर्वात में सबसे अधिक होता है , किसी माध्यम के लिए –
F = F0/F = नियतांक = K = माध्यम का पराविद्युतांक
F0 व F का मान रखने पर –
ε/ε0 = K = माध्यम का पराविद्युतांक
ε = ε0 K
यह निर्वात की विद्युतशीलता (ε0) और माध्यम की निरपेक्ष विधुतशीलता (ε) के बीच सम्बन्ध पाया जाता है।
अत: कूलाम बल के लिए व्यापक सूत्र निम्न प्राप्त होता है –

K का मान निर्वात के लिए 1 होता है जो कि K का न्यूनतम मान है। वायु के लिए K का मान 1.00054 होता है। K का मान सभी कुचालक पदार्थों के लिए 1 से अधिक होता है उदाहरण के लिए पानी के लिए K का मान 80 तथा कागज के लिए K का मान 3.5 होता है। धातुओं के लिए K का मान अन्नत होता है क्योंकि आवेशों के मध्य धातु रखने पर उन आवेशो के मध्य कार्यरत बल का मान शून्य होता है।
आवेश के मात्रक (कुलाम) की परिभाषा : कुलाम के नियम के अनुसार निर्वात में दो आवेशो के बीच लगने वाला बल –
F = Kq1q2/r2
माना q1 = q2 = 1C तथा r = 1 मीटर
तो F = K
चूँकि K = 9 x 109 न्यूटन.मीटर2/कूलाम2
अर्थात F = 9 x 109
अत: यदि निर्वात में एक मीटर की दूरी पर रखे दो समान परिमाण के आवेशो के बीच 9 x 109 न्यूटन का वैद्युत बल कार्य करे तो प्रत्येक आवेश एक कुलाम के बराबर होगा।
कुलाम के नियम का महत्व :
कूलाम के नियम के द्वारा निम्नलिखित बलों को सफलता पूर्वक समझाया जा सकता है –
- अणु बनाने वाले परमाणुओं के मध्य बंधन बल की व्याख्या इसके द्वारा की जा सकती है।
- किसी परमाणु के नाभिक और उसके चारों ओर घुमने वाले इलेक्ट्रॉनों के बीच लगने वाला बल को कुलाम के नियम से समझाया जा सकता है।
- अणुओं अथवा परमाणुओं को परस्पर सम्बद्ध कर द्रव या ठोस बनाने वाले बल।
निर्वात की विद्युतशीलता (ε0) का मात्रक = C2N-1m-2 या कुलाम2/न्यूटन.मीटर2
निर्वात की विद्युतशीलता (ε0) की विमा (विमीय सूत्र) = [M-1L-3T4A2]
कुलॉम का नियम : दो स्थिर बिंदु आवेशो के मध्य आकर्षण या विकर्षण का बल , आवेशो के गुणनफल के समानुपाती और उनके मध्य की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह बल दोनों आवेशों को मिलाने वाली रेखा के अनुदिश लगता है।
यदि आवेशो का परिमाण q1 व q2 एवं उनके मध्य की दूरी r है तो उनके मध्य लगने वाला बल F है तो –
F ∝ q1q2
F ∝ 1/r2
अत: F ∝ q1q2/r2
अर्थात F = C q1q2/r2
यहाँ C नियतांक है जो दोनों आवेशों के मध्य स्थित माध्यम तथा चयन की गयी इकाइयों पर निर्भर करता है।
C = 1/4πε0 = 9 x 109 न्यूटन.मीटर2/कूलाम2 (SI मात्रक)
C = 1 (esu मात्रक या स्थिर वैद्युत मात्रक में)
ε0 = 8.85 x 10-12 कूलाम2/न्यूटन.मीटर2 = मुक्तावकाश की पारगम्यता
माध्यम का प्रभाव : किसी माध्यम का परावैद्युतांक किसी निश्चित दूरी पर स्थित बिंदु आवेशों के मध्य वायु में लगने वाले बल तथा समान दूरी पर स्थित उस माध्यम में उन आवेशों पर लगने वाले बल का अनुपात के तुल्य होता है।
Fवायु = q1q2/4π ε0r2
Fमाध्यम = q1q2/4π ε0εrr2
Fमाध्यम/ Fवायु = 1/εr = K
εr या K = परावैद्युतांक या सापेक्ष पारगम्यता या माध्यम की विशिष्ट प्रेरणिक क्षमता है।
पारगम्यता : माध्यम के चारों ओर स्थित विद्युत आवेशो के कारण माध्यम से गुजरने वाली विद्युत बल रेखाओ के माध्यम से गुजरने की क्षमता उस माध्यम की पारगम्यता का मापदण्ड होती है , यह आवेशो के मध्य लगने वाले बलों को व्यक्त करती है।
आपेक्षिक पारगम्यता : किसी माध्यम की आपेक्षिक पारगम्यता या परावैध्युतांक (εr या K ) माध्यम की पारगम्यता ε तथा मुक्तावकाश की पारगम्यता ε0 के अनुपात के तुल्य होती है।
εr या K = ε/ε0
पारगम्यता की विमाएँ ε0 = आवेश2/बल x लम्बाई2
= T2A2/MLT-2L2
= M-1L-3T4A2
विभिन्न माध्यमों के पराविद्युतांक :
निर्वात = 1
वायु = 1.00059
जल = 80
अभ्रक = 6
टेफ़लोन = 2
काँच = 5 से 10
प्लास्टिक = 4.5
धातुएँ = ∞
विद्युत बल के नियम या कूलम्ब का नियम– दो समान आवेशों के बीच प्रतिकर्षण और दो असमान आवेशों के बीच आकर्षण का बल कार्य करता है। यह बल दोनों आवेशों के परिमाण, उनके बीच की दूरी तथा उनके बीच के माध्यम की प्रकृति पर निर्भर करता है। कुलम्ब ने अपने प्रयोगों के आधार पर दो आवेशों के बीच कार्य करने वाले बल के लिए दो नियम प्रतिपादित किए
– दो आवेशों के बीच आकर्षण अथवा प्रतिकर्षण का बल उनके आवेशों के गुणनफल का अनुक्रमानुपाती होता है।
– दो आवेशों के बीच आकर्षण या विकर्षण का बल आवेशो के बीच की दूरी के वर्ग का व्युत्क्रमानुपाती होता है। यह नियम व्युत्क्रम-वर्ग-नियम कहलाता है।
विद्युत विभव- एकांक धन आवेश को अनन्त से विद्युत क्षेत्र के किसी बिन्दु तक लाने में जो कार्य करना पड़ता है, उसे विद्युत विभव कहते है। अर्थात विद्युत विभव किसी धनात्मक परीक्षण आवेश को अनन्त से विद्युत क्षेत्र के किसी बिन्दु तक लाने में किए गए कार्य (ॅ) एवं परीक्षण आवेश के मान (ु0) की निष्पत्ति है। अतः
विद्युत विभव, ट = ॅध् ु0
विद्युत विभव का ैप् मात्रक जूल प्रति कूलम्ब होता है, जिसे वोल्ट भी कहते हैं। विभव का मात्रक वोल्ट इटली के प्रसिद्ध वैज्ञानिक एलसेन्ड्रो वोल्टा के सम्मान में रखा गया है। विभव एक अदिश राशि है।
विभवान्तर– एक कूलम्ब धनात्मक आवेश को विद्युत क्षेत्र में एक बिन्दु से दूसरे बिन्दु तक ले जाने मे किए गए कार्य को उन बिन्दुओं में मध्य विभवान्तर कहते है। विभवान्तर का मात्रक भी वोल्ट होता है तथा यह भी एक अदिश राशि हैं।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics