coefficient of self inductance in hindi self induction स्वप्रेरण गुणांक या स्वप्रेरकत्व क्या है ? किसे कहते है ?
परिभाषा : माना किसी N फेरो वाली कुण्डली में I धारा प्रवाहित हो रही है , I धारा प्रवाहित होने से इस कुण्डली के प्रत्येक फेरे के कारण ϴ चुम्बकीय फ्लक्स उत्पन्न हो जाता है।
अतः सम्पूर्ण फेरों या कुण्डली के कारण कुल उत्पन्न चुम्बकीय फ्लक्स का मान Nϴ होगा।
कुण्डली में उत्पन्न चुम्बकीय फ्लक्स Nϴ का मान इसमें प्रवाहित धारा के समानुपाती होती है।
अतः
Nϴ ∝ I
समानुपाती का चिन्ह हटाने पर
Nϴ = LI
यहाँ L एक समानुपाती गुणांक (नियतांक) है , इसे स्वप्रेरण गुणांक या स्वप्रेरकत्व कहा जाता है।
L का मान कुण्डली में लिपटे फेरों की संख्या , आकृति , आकार , माध्यम क्रोड़ पदार्थ पर निर्भर करता है।
यदि N = 1 तथा I = 1 तो
ϴ = I
परिभाषा : किसी कुण्डली का स्वप्रेरण गुणांक उस चुम्बकीय फ्लक्स के बराबर होता है जो उस कुण्डली में 1 एम्पियर की धारा प्रवाहित करने पर उत्पन्न होता है।
माना कुण्डली में धारा परिवर्तनशील है अर्थात धारा का मान △t समय में I1 से बदलकर I2 हो जाता है। तो कुण्डली में उत्पन्न प्राम्भिक चुम्बकीय फ्लक्स का मान जब धारा I1 बह रही है।
Nϴ1 = LI1
△t समय बाद कुण्डली से सम्बद्ध चुम्बकीय फ्लक्स जब धारा I2 बह रही है।
Nϴ2 = LI2
△t समय में फ्लक्स में परिवर्तन
N△ϴ = Nϴ2 – Nϴ1
N△ϴ = LI2 – LI1
N△ϴ = L△I
अतः चुंबकीय फ्लक्स में परिवर्तन की दर
N△ϴ/△t = L△I/△t
फैराडे के चुम्बकीय प्रेरण के नियम से
समीकरण में मान रखने पर
E = –L△I/△t
यहाँ ऋणात्मक चिन्ह यह दर्शाता है की प्रेरित विद्युत वाहक बल मूल धारा I में परिवर्तन का विरोध करती है।
यदि △I/△t = 1 हो तो
E = -L
अतः ” किसी कुण्डली का स्वप्रेरण गुणांक उस कुण्डली में उत्पन्न प्रेरित विद्युत वाहक बल के बराबर होती है जब धारा परिवर्तन की दर 1 एम्पियर प्रति सेकंड हो। “
हमने देखा की प्रेरित विद्युत वाहक बल कुण्डली में धारा का विरोध करता है अत: कुण्डली में धारा प्रवाहन के लिए इस प्रेरित विद्युत वाहक बल के विरुद्ध एक बाह्य कार्य करना पड़ता है , यह कार्य कुण्डली में चुम्बकीय स्थितिज उर्जा के रूप में संचित हो जाता है , जिसका मान निम्न प्रकार दिया जाता है
W = LI2/2
यदि I = L = 1 तो W = 2
अत: कुण्डली में प्रेरित विद्युत वाहक बल के विरुद्ध किया गया कार्य स्वप्रेरकत्व का दोगुना होता है।
प्रेरकत्व एक अदिश राशि है तथा इसका SI मात्रक हेनरी होता है।
इसकी विमा [M1L2T-2A-2] होती है।
स्वप्रेरण गुणांक या स्वप्रेरकत्व (coefficient of self induction or self inductance in hindi) : माना N फेरों वाली कुण्डली में i धारा बहने से प्रत्येक फेरे से सम्बद्ध चुम्बकीय फ्लक्स ϕ है , अत: कुण्डली के साथ सम्बद्ध कुल चुम्बकीय फ्लक्स Nϕ होगा। इस फ्लक्स का मान कुंडली में बहने वाली धारा के अनुक्रमानुपाती होता है अर्थात
Nϕ ∝ i
या
Nϕ = L.i . . . . . . . . . .. समीकरण-1
यहाँ L , एक नियतांक है जिसे “स्वप्रेरण गुणांक” अथवा “स्वप्रेरकत्व” कहते है।
समीकरण-1 से –
L = Nϕ/i . . . . . . . . . .. समीकरण-2
यदि धारा i = 1 एम्पियर तो L = Nϕ
अर्थात किसी कुण्डली का स्वप्रेरण गुणांक उस चुम्बकीय फ्लक्स के तुल्य है जो उस कुंडली में एक एम्पियर धारा बहने पर उसके साथ सम्बद्ध होता है।
यदि कुंडली में बहने वाली धारा △t समय में i1 से बदलकर i2 हो जाती है तो कुण्डली से सम्बद्ध प्रारंभिक चुम्बकीय फ्लक्स समीकरण- 1 से –
Nϕ1 = L.i1
तथा अंतिम चुम्बकीय फ्लक्स –
Nϕ2 = L.i2
अत: फ्लक्स परिवर्तन
N△ϕ = Nϕ2 – Nϕ1
N△ϕ = L.i2 – L.i1
N△ϕ = L(i2 – i1)
अत:
N△ϕ = L△i
अत: फ्लक्स परिवर्तन की दर –
N△ϕ/△t = L△i/△t
अत: कुण्डली में स्वप्रेरित विद्युत वाहक बल –
eL = -N△ϕ/△t
अथवा
eL = -L△i/△t . . . . . . . . . .. समीकरण-3
यदि धारा परिवर्तन की दर △i/△t = 1 A/s हो तो
eL = -L
या संख्यात्मक रूप से eL = L
अर्थात किसी कुण्डली का स्वप्रेरण गुणांक उस विद्युत वाहक बल के तुल्य है जो उस कुण्डली में 1 A/s की दर से विद्युत धारा बदलने पर उसमें उत्पन्न होता है।
स्वप्रेरण गुणांक या स्वप्रेरकत्व का मात्रक (unit of self inductance)
L का मात्रक = V.s/A
= V.s.A-1
अर्थात L का मात्रक V.s.A-1 है जिसे हेनरी भी कहते है अत:
1 V.s.A-1 = 1 H
व्यवहार में प्रेरकत्व के छोटे मात्रक भी प्रयुक्त होते है , जैसे –
1 मिली हेनरी (mH) = 10-3
H
1 माइक्रो हेनरी (uH) = 10–6 H
स्वप्रेरकत्व के मात्रक हेनरी की परिभाषा –
समीकरण-2 से –
L = Nϕ/i
यदि धारा i = 1 एम्पियर ; Nϕ = 1 वेबर तो L = 1 H (हेनरी)
अर्थात यदि किसी कुण्डली में एक एम्पियर की धारा बहने पर उसके साथ एक वेबर का चुम्बकीय फ्लक्स सम्बद्ध होता है तो उस कुण्डली का स्वप्रेरकत्व एक हेनरी होगा।
समीकरण-3 से –
L = -eL/(△i/△t)
L = -eL/(△i/△t)
(संख्यात्मक रूप से)
यदि △i/△t = 1 As-1 ; eL
= 1 वोल्ट तो L = 1 हेनरी
अर्थात यदि किसी कुंडली में 1 As-1 की दर से धारा बदलने पर उसमें 1 वोल्ट का स्वप्रेरित विद्युत वाहक बल उत्पन्न होता है तो उसका स्वप्रेरकत्व एक हेनरी होगा।
स्वप्रेरकत्व की विमीय सूत्र –
L का विमीय सूत्र –
L की विमा = [M1L2T-2A-2]
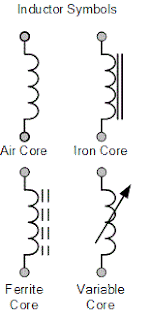
स्वप्रेरकत्व का निरूपण – विभिन्न प्रकार के स्वप्रेरणत्व निम्न चित्र में प्रदर्शित किये गए है –
नोट : एक आदर्श प्रेरकत्व का स्वप्रेरकत्व अधिक होता है और उसका प्रतिरोध शून्य ओम होता है।
युग्मन गुणांक (coefficient of coupling) – जब दो कुण्डली जिनके प्रेरकत्व (L1
और L2 है तथा अन्योन्य प्रेरकत्व M हो तो युग्मन गुणांक)
K = M/√L1L2
K – 0 = जब दोनों कुण्डलियों का युग्म ढीला होता है।
K – 1 = जब दोनों कुंडलियो का युग्म कसा होता है।
समतल कुण्डली का स्वप्रेरकत्व (self inductance of a plane coil)
माना N फेरों वाली एक समतल कुंडली की त्रिज्या r है तथा इसमें i एम्पियर की धारा प्रवाहित हो रही है। इस कुण्डली के केंद्र पर उत्पन्न चुम्बकीय क्षेत्र की तीव्रता B = u0.N.i/2r
यदि इस क्षेत्र को कुण्डली के सम्पूर्ण तल में एक समान मानें तो कुंडली से सम्बद्ध चुम्बकीय फ्लक्स
Nϕ = N.(BA) = N.B.πr2
अथवा Nϕ = N.u0N.i. πr2/2r
अथवा
Nϕ = u0πN2i.r/2 . . . . . . . . . . . . समीकरण-1
यदि कुण्डली का स्वप्रेरकत्व L हो तो
L = Nϕ/i . . . . . . . . . . . . समीकरण-2
समीकरण-2 में Nϕ का मान समीकरण-1 से रखने पर –
L = u0πN2.r/2 हेनरी . . . . . . . . . . . . समीकरण-3
समीकरण-3 से स्पष्ट है कि u0 का मात्रक हेनरी/मीटर भी लिखा जा सकता है।
किसी कुण्डली का स्वप्रेरकत्व कुंडली के अन्दर रखे कोड के पदार्थ पर भी निर्भर करता है। यदि कुण्डली के अन्दर किसी लौह चुम्बकीय पदार्थ जैसे लोहा , निकल अथवा कोबाल्ट की छड़ रख दी जाए तो स्वप्रेरण गुणांक L का मान बहुत अधिक हो जाता है। इसे एक सरल प्रयोग द्वारा प्रदर्शित किया जा सकता है। काफी अधिक चक्करों वाली एक कुण्डली को 220 वोल्ट वाले विद्युत बल्ब के साथ श्रेणीबद्ध करके AC स्रोत से जोड़ दिया जाए तो बल्ब चमकने लगता है। अब यदि कुण्डली को बिना स्पर्श किये उसके अन्दर लोहे की छड लायी जाए तो बल्ब की चमक तुरंत काफी कम हो जाती है। इसी प्रकार यदि लोहे की कई छड़े एक एक करके कुण्डली के अन्दर लायी जाए तो बल्ब की चमक क्रमशः कम होती जाती है। स्मरणीय है कि इस प्रयोग में AC स्रोत ही लेना है क्योंकि प्रेरण की घटना तभी तक होती है जब तक धारा परिवर्तित रहती है। दिष्ट धारा नियत रहती है , अत: प्रेरण प्रभाव परिलक्षित नहीं होगा।