सममितता केन्द्र , सममितता तल , सममितता अक्ष , सममितता अवयव (centre of symmetry in hindi)
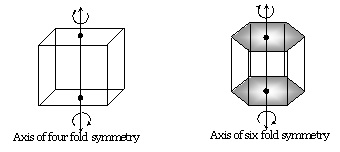
अर्थात किसी क्रिस्टल में स्थित वह बिंदु जिससे सभी तरफ क्रिस्टल के पृष्ठ की दूरी बराबर हो , उस बिंदु को सममितता केन्द्र कहा जाता है।
चित्र में सममितता केन्द्र को बिंदु से दर्शाया हुआ है , घन का सममितता केन्द्र इसके केंद्र में स्थित होता है। याद रखे की किसी भी क्रिस्टल का सममितता केन्द्र केवल एक हो सकता है , एक से अधिक सममितता केन्द्र संभव नहीं है तथा कई क्रिस्टल ऐसी भी होते है जिनका कोई सममितता केन्द्र नहीं होता है।
सममितता तल (Plane of symmetry)
सममितता अक्ष (Axis of symmetry)
सममितता अवयव (elements of symmetry)
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics



