ब्रैग समीकरण किसे कहते हैं , Bragg’s Equation in hindi सिद्धांत किसने दिया था उपयोग एक्स रे विवर्तन और ब्रैग के समीकरण

एक्स रे विवर्तन और ब्रैग के समीकरण ब्रैग समीकरण किसे कहते हैं , Bragg’s Equation in hindi सिद्धांत किसने दिया था ?

ब्रैग समीकरण (Bragg’s Equation)

डब्ल्यू. एच. बॅग (W. H. Bragg) एवं उनके पुत्र डब्ल्यू. एल. बॅग (W. L. Bragg) ने 1912 में क्रिस्टलों द्वारा x-किरणों के विवर्तन का सरल स्पष्टीकरण दिया। उनके अनुसार जब किसी क्रिस्टल पर x-किरणों का पुंज (beam) टकराता है तो उसका प्रत्येक परमाणु उसी तरंग-दैर्घ्य वाले प्रकीर्णित प्रकाश के स्रोत के रूप में कार्य करता है। उन्होंने X-किरणों की तरंग दैर्घ्य और जालक तलों के बीच की दूरी में एक सम्बन्ध स्थापित किया। चूंकि क्रिस्टलों में परमाणु (अथवा आयन) एक क्रमबद्ध व्यवस्था में रहते हैं, अतः उनके तलों पर X-किरणें बिल्कुल उसी प्रकार परावर्तित हो जाती हैं जिस प्रकार प्रकाश की किरणें समतल दर्पण से परावर्तित हो जाती हैं।

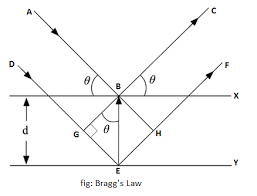
माना कि AA’, BB’, cc’, आदि OM समान दूरी पर स्थित किसी क्रिस्टल के जालक Rota तल (Lattice planes) अथवा बैग तल (Bragg’s planes) हैं जिनके बीच की दूरी d है। माना कि तरंग-दैर्घ्य की X-किरणों का पुंज P, तल AA’ पर बिन्दु Q पर तथा तल BB’ पर बिन्दु R पर टकराता है और परावर्तित होकर क्रमशः 0′ व R’ की दिशा में चला जाता है। QQ’ तथा RR’ एक-दूसरे के समानान्तर हैं अतः PRB तथा PQA और परावर्तित कोण QQA’ तथा RRB’ एक-दूसरे के समान होंगे। माना इस कोण का मान 0 है। अब यदि OR दोनों तलों पर लम्ब (perpendicular) हो और XOY दोनों परावर्तित किरणों पर लम्ब हो तब दोनों परावर्तित किरणों QQ’ तथा RR’ के पथ का अन्तर (Path difference)

QR = QRY – QX B .

चूंकि Qx = QN

अतः पथान्तर = QRY – QN= NRY = 2RY

ROY से, RY = d sine अतः पथान्तर =2d sin Φ …(3)

यदि पथान्तर तरंग-दैर्ध्य का गुणांक हो तो परावर्तित किरण का संपोषी व्यतिकरण होगा। अत: अधि तीव्रता वाली x-किरणों के लिए

2d sin e =nλ ……………….(4)

यहां n एक पूर्णाक अर्थात् 1, 2, 3…… है। इस समीकरण को बैग की समीकरण (Bragg’s equation) कहते हैं। sine का मान एक (one) से अधिक नहीं हो सकता अतः उस स्थिति में दो तलों के मध्य की दूरी कम-से-कम (minimum) होगी। अर्थात्

2dmin = nλ

अथवा d_min = nλ/2

इस प्रकार किन्हीं दो सतहों के बीच की दूरी को हम इस विधि द्वारा ज्ञात कर सकते हैं।

उदाहरण 5.8.x-किरणों का प्रथम कोटि परावर्तन NaCl के (200) फलक से 5°9′ कोण पर होता है। यदि x-किरणों का तरंगदैर्घ्य 0.58 A हो तो NaCl क्रिस्टल के (200) तलों के अन्तराल का परिकलन कीजिए। [sin 59′ = 0.103]

हल : 2d sin Φ = nλ

मान रखने पर – 2 x d x 0.103 =1×0.58A

D = 0.58/2 x 0.103 = 2.816 A = 2.816 x 10^-8 cm

एक घन इकाई कोशिका में कणों का निर्धारण (DETERMINATION OF PARTICLES IN A UNIT OF CUBIC CELL)

उपर्युक्त विवरण से स्पष्ट है कि किसी त्रिविमीय जालक (space lattice) अथवा इकाई जालक (unit lattice) में कम-से-कम 8 कण (अण, परमाण अथवा आयन) व्यवस्थित है और अधिक-से-अधिक 14 कण व्यवस्थित है और असंख्य इकाई जालक एक व्यवस्थित क्रम में एकत्रित होकर एक क्रिस्टल का निर्माण करते हैं। अब प्रश्न उठता है कि एक इकाई कोशिका में कितने कणों को माना जाये। उदाहरण के लिए, एक घन इकाई कोशिका के कणों का निर्धारण हम निम्न प्रकार से कर सकते हैं

(1) घन इकाई जालक का जो कोने वाला कण है वह उन सब इकाई कोशिकाओं (unit cells) के साझे में होता है जो उस इकाई बिन्दु पर मिलती हैं। एक त्रिविमीय संरचना में इस बिन्दु पर आठ इकाई घन कोशिकाएं स्पर्श करती हैं अर्थात् यह कण आठ इकाई कोशिकाओं के साझे में है। दूसरे शब्दों में, इस कण का भाग प्रत्येक इकाई कोशिका के हिस्से का है। बामा एक सरल घनीय जालक में चूंकि कुल आठ कण होते हैं, और प्रत्येक कण का योगदान है, अतः हम कह सकते हैं कि एक सरल घनीय क्रिस्टल की इकाई कोशिका में कुल एक ही कण विद्यमान है। इस प्रकार की क्रिस्टल संरचना अधिक सामान्य नहीं है और केवल एक धातु पोलोनियम (Po) में पायी जाती है।

(2) एक फलककेन्द्रित कण दो इकाई कोशिकाओं के फलकों के सम्पर्क में रहता है अर्थात् यह दो इकाई कोशिकाओं के साझे में है अतः प्रत्येक इकाई में इस कण का योगदान : भाग हुआ। प्रत्येक फलक केन्द्रित घनीय FCC जालक में आठ तो कोने वाले कण होंगे जिनमें से प्रत्येक का योगदान होगा और इसमें छः फलककेन्द्रित कण होंगे जिनमें से प्रत्येक का योगदान होगा। अतः एक फलककेन्द्रित घनीय क्रिस्टल की इकाई कोशिका में विद्यमान कणों की संख्या (1/8 x 8 + ½ x 6 = 1 +3) चार होगी।

(3) एक कायकेन्द्रित कण उस इकाई जालक के मध्य में होता है अतः उसका कोई साझेदार नहीं होता फलतः वह पूर्णतः उस इकाई कोशिका का होगा। इस प्रकार एक कायकेन्द्रित घनीय BBC क्रिस्टल की इकाई कोशिका में विद्यमान कुल कणों की संख्या दो होगी. क्योंकि इसके भी योगदान देने वाले आठ कोने वाले कण हैं, जिनका इकाई कोशिका को कुल योगदान एक कण का होगा और एक कण इसके मध्य वाला जिसका पूरा योगदान इस इकाई को होगा। इस प्रकार संक्षेप में हम कह सकते हैं कि

(i) एक सरल घन की इकाई कोशिका में कणों की संख्या=1

(ii) एक BCC की इकाई कोशिका में कणों की संख्या = 2 और

(ii) एक FCC की इकाई कोशिका में कणों की संख्या = 4

इसके आधार पर हम किसी इकाई कोशिका का घनत्व भी ज्ञात कर सकते हैं। इसके लिए निम्न सूत्र प्रयुक्त करते हैं

D = Z xM/ N₀ X a³ …(2)

जहां Z = एक इकाई कोशिका में कणों की संख्या

M = उस कण का द्रव्यमान

No = ऐवोगैड्रो संख्या

a = इकाई कोशिका के किनारे की लम्बाई

उदाहरण : एक धात्विक तत्व की क्रिस्टल जालक घनीय है। एकक सेल के प्रत्येक किनारे की लम्बाई 2A है। धातु का घनत्व 2.5 gm cm-3 है। 200g धातु में एकक सेल की संख्या बताइए।)

हल : (i) एकक सेल का आयतन a³ = (2A)³ = 8A³ = 8 x 10^-24 cm³

(ii) 200 g धातु का आयतन (V) = m /p = 208g/2.5 g cm^-3 = 40 cm³

(iii) 200g धातु में एकक सेलों की संख्या = 40 cm³/8 x 10^-24 cm³ = 5 x 10²⁴ उत्तर क्रिस्टला द्वारा X-किरणों का विवर्तन (X-RAYS DIFFRACTION BY CRYSTALS)

x-किरणों की सहायता से क्रिस्टलों की आन्तरिक संरचना के बारे में ज्ञात किया जा सकता है। X-किरणें प्रकाश व ध्वनि की भांति तरंग गति से चलने वाली ऊर्जा की किरणें होती हैं जिनकी तरंग-दैर्घ्य (wave-length) बहुत कम 10-8 के क्रम (order) की होती है। किसी क्रिस्टल की सतहें (planes) x-किरणों के प्रति बिल्कुल ऐसा व्यवहार करती हैं जैसा कि कोई समतल दर्पण प्रकाश की किरणों के प्रति करता है।