बायो सावर्ट का नियम क्या है Biot Savart’s law in hindi , चुंबकशीलता या चुंबकीय पारगम्यता बायो सेवर्ट
Biot Savart’s law in hindi बायो सावर्ट का नियम क्या है बायो सेवर्ट का नियम का सूत्र किसे कहते है ? स्टेटमेंट formula , विमा और मात्रक लिखिए biot savart law in hindi for class 12 physics notes |
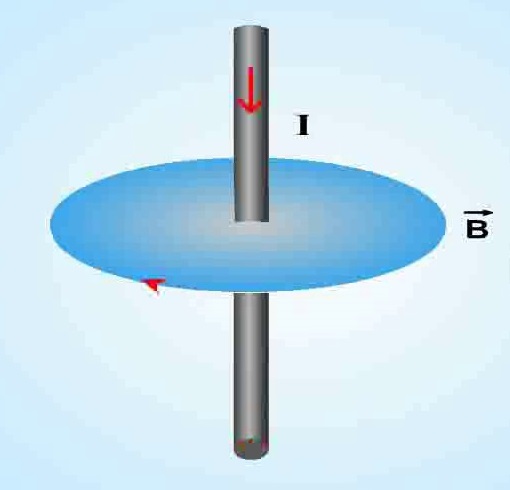
प्रस्तावना : हम ओरस्टेड का प्रयोग के बारे में पढ़ चुके है जिसमे उन्होंने यह बताया की जब किसी चालक में धारा प्रवाहित की जाती है तो चालक के चारों पर एक चुंबकीय क्षेत्र उत्पन्न हो जाता है तथा इस क्षेत्र की रेखाएं संकेन्द्रिय वृतो के रूप में होती है।
धारावाही चालक पर चुम्बकीय क्षेत्र में बल के लिए व्यंजक (expression for the force in magnetic field due to current carrying conductor) : किसी चालक में मुक्त इलेक्ट्रॉनों की संख्या काफी अधिक होती है। ये इलेक्ट्रॉन चालक में प्रवाहित परम्परागत धारा की दिशा के विपरीत अनुगमन वेग vd से गति करते है। किसी समरूप चुम्बकीय क्षेत्र में गति करने पर ये इलेक्ट्रॉन विक्षेपण बल का अनुभव करते है जो चालक को स्थानांतरित करता है।
माना l लम्बाई का एक चालक एक समान चुम्बकीय क्षेत्र B में क्षेत्र की दिशा के साथ θ कोण पर स्थित है तथा चालक में I धारा प्रवाहित होती है।
चालक का अनुप्रस्थ काट परिच्छेद क्षेत्रफल A है तथा चालक के प्रति एकांक आयतन में मुक्त इलेक्ट्रॉनों की संख्या n है।
चूँकि लोरेन्ज बल –
Fm = q(v x B)
अत: चालक में गतिशील एक इलेक्ट्रॉन पर लोरेन्ज बल –
Fm = -e(vd x B) . . . . . . .. . . समीकरण-1
चुम्बकीय बल Fm की दिशा v तथा B के तल के लम्बवत होती है।
यदि चालक के dl लम्बाई के अल्पांश पर विचार करे तो इस अल्पांश में।
मुक्त इलेक्ट्रॉनों की संख्या n’ = n x अल्पांश का आयतन
अथवा n’ = n x A.dl
या n’ = nA.dl
अत: समीकरण-1 से अल्पांश पर लगने वाला चुम्बकीय बल –
dFm = n’e(vd x B)
या
dFm = -Ane.dl(Vd x B) . . . . . . .. . . समीकरण-2
अत: अनुगमन वेग Vd = -dl/dt
(यहाँ ऋण चिन्ह का प्रयोग इसलिए किया गया है क्योंकि dl और vd परस्पर विपरीत दिशा में है )
अत: समीकरण-2 से
dFm = -Ane.dl(-dl/dt x B)
अथवा
dFm = Ane.dl/dt (dl x B) . . . . . . .. . . समीकरण-3
लेकिन धारा i = dq/dt
जहाँ dq अल्पांश का मुक्त आवेश है।
अत: I = Ane.dl/dt
अत: समीकरण-3 से ,
dFm = I.(dl x B)
अत: चालक इसी प्रकार के अनेकों अल्पांशों से मिलकर बना है अत: सम्पूर्ण चालक पर लगने वाला बल सभी अल्पांशो पर लगने वाले बलों का योग होगा।
अत: पूरे चालक पर लगने वाला बल –
F = ∫dFm = ∫I.(dl x B) = ∫dI(l x B)
अत: चुम्बकीय क्षेत्र B नियत है अत: उसका अवकलन शून्य होगा।
अत: F = I.(l x B)
अथवा
F = I.lBsinθ.n
यहाँ n कैप = l और B के तल के लम्बवत दिशा में एकांक वेक्टर।
या
F = I.lBsinθ
चुम्बकीय क्षेत्र के साथ धारावाही चालक के कोण पर यह बल निर्भर करेगा।
(i) जब θ = 0 या θ = 180 डिग्री अर्थात धारावाही चालक चुम्बकीय क्षेत्र के अनुदिश है अथवा विपरीत दिशा में है तो
sinθ = 0
अत: F = 0
(ii) जब θ = 90 डिग्री अर्थात धारावाही चालक चुम्बकीय क्षेत्र के लम्बवत स्थित है तो
sinθ = 1 जो कि sinθ का अधिकतम मान है।
Fmax = IBl
प्रश्न 1 : एक 2m लम्बे तार में 4A की धारा वह रही है। तार 2 wb.m-2 के चुम्बकीय क्षेत्र में क्षेत्र से 30 डिग्री के कोण पर रखा है , तार पर कितना बल लगेगा ?
उत्तर : धारावाही चालक पर चुम्बकीय क्षेत्र में बल F = I.lBsinθ
मान रखकर हल करने पर –
F = 8 N
प्रश्न 2 : 40 सेंटीमीटर लम्बे एक तार में 2.5 A की धारा बह रही है। तार 8 x 10-3 Wb.m-2 के चुम्बकीय क्षेत्र के लम्बवत रखा गया है। इस पर लगने वाले बल का परिमाण ज्ञात कीजिये।
उत्तर : धारावाही चालक पर चुम्बकीय क्षेत्र में लगने वाला बल F = I.lBsinθ
F = 8 x 10-3 N
बायोसावर्ट का नियम (biot savart’s law statement)
ऑर्स्टेड के प्रयोग से ज्ञात हुआ कि जब किसी चालक में धारा बहाई जाती है तो चालक के परित: एक चुम्बकीय क्षेत्र उत्पन्न होता है जिसकी बल रेखाएं समकेन्द्रीय वृत्तों के रूप में होती है। किसी धारावाही चालक के कारण उत्पन्न चुम्बकीय क्षेत्र को ज्ञात करने के लिए चालक को अनेक छोटे छोटे अल्पांशो में बाँट लेते है तथा सभी अल्पांशो के कारण उत्पन्न चुम्बकीय क्षेत्रों को जोड़कर कुल चुम्बकीय क्षेत्र ज्ञात करते है। सन 1820 में फ्रांसीसी वैज्ञानिक बायोसावर्ट ने किसी धारावाही चालक के विभिन्न अल्पांश के कारण किसी बिंदु पर उत्पन्न चुम्बकीय क्षेत्र का अध्ययन किया तथा प्राप्त निष्कर्षों को एक नियम के रूप में प्रस्तुत किया जो बायो सावर्ट नियम के रूप में जाना गया।
माना एक धारावाही चालक XY में I धारा प्रवाहित हो रही है तथा उसके अल्पांश ab (जिसकी लम्बाई dl है) के कारण अल्पांश के मध्य बिंदु O से θ दिशा में r दूरी पर स्थित बिंदु P पर उत्पन्न चुम्बकीय क्षेत्र पर विचार करना है। बायो सावर्ट के नियमानुसार P पर उत्पन्न चुम्बकीय क्षेत्र dB निम्नलिखित चार बातों पर निर्भर करता है –
(i) dB का मान चालक में प्रवाहित धारा के अनुक्रमानुपाती होता है अर्थात
dB ∝ I
(ii) dB का मान अल्पांश ab की लम्बाई के अनुक्रमानुपाती होता है , अर्थात
dB ∝ dl
(iii) dB का मान अल्पांश के साथ P की दिशा बताने वाले कोण को ज्या (sinθ) के अनुक्रमानुपाती होता है –
अर्थात
dB ∝ sinθ
(iv) dB का मान अल्पांश से P की दूरी r के वर्ग के व्युत्क्रमानुपाती होता है अर्थात –
dB ∝ 1/r2
उक्त चारों समीकरणों को मिलाने पर –
dB ∝ I.dl.sinθ/r2
dB = KI.dl.sinθ/r2
यहाँ K एक नियतांक है। यदि चालक निर्वात अथवा वायु में रखा है तो
K = u0/4π = 10-7
यहाँ u0 = निर्वात की चुम्बकशीलता
अत:
dB = (u0/4π)I.dl.sinθ/r2
निम्न समीकरण को निम्नलिखित प्रकार से भी व्यक्त कर सकते है –
dB = (10-7)I.dl.sinθ/r2
निम्न सम्बन्ध को ही बायो सावर्ट का नियम कहते है।
धारावाही चालक और बिंदु P कागज के तल में है। धारावाही चालक के अल्पांश ab के कारण बिंदु P पर उत्पन्न चुम्बकीय क्षेत्र की दिशा कागज के तल के लम्बवत नीचे की ओर होगी। इसे बिन्दु (x) द्वारा प्रदर्शित किया गया है और चिन्ह (.) चुम्बकीय क्षेत्र को लम्बवत बाहर की ओर प्रदर्शित करता है।
बायो-सावर्ट के नियम को ही “लाप्लास का नियम (laplace’s law) ” या “एम्पियर का नियम (ampere’s law)” कहते है।
धारावाही चालक के कारण उत्पन्न चुम्बकीय क्षेत्र की दिशा ज्ञात करने के नियम हम पढ़ चुके है।
सम्पूर्ण धारावाही चालक के कारण उत्पन्न चुम्बकीय क्षेत्र ज्ञात करने के लिए उसके समस्त अल्पांशो के कारण P पर उत्पन्न चुम्बकीय क्षेत्रों को जोड़ना होगा अर्थात सम्पूर्ण चालक के कारण उत्पन्न क्षेत्र
B = ∫dB = ∫(u0/4π)I.dl.sinθ/r2
निर्वात की चुम्बकशीलता (permeability of free space) (μ0)
(1) मात्रक =
चूँकि dB = (u0/4π)I.dl.sinθ/r2
u0 = dB4πr2/I.dl.sinθ
चूँकि 4π और sinθ के मात्रक नहीं है।
अत: निर्वात की चुम्बकशीलता (u0) का मात्रक = Kg.ms-2.A-2
(2) निर्वात की चुम्बकशीलता (u0) का विमीय सूत्र –
चूँकि (u0) का मात्रक = Kg.ms-2.A-2
अत: (u0) का विमीय सूत्र = [M1L1T-2A-2]
(3) निर्वात की चुम्बकशीलता (u0) का आंकिक मान –
चूँकि u0/4π = 10-7 (यदि i को एम्पियर और dl , r को मीटर में व्यक्त करे )
u0 = 4π x 10-7 N.A-2
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics



