आरेनियस समीकरण (arrhenius equation in hindi) , संक्रमण अवस्था (transition state in hindi)
संक्रमण अवस्था (transition state) : किसी रासायनिक अभिक्रिया में अभिकारक अणुओं को उत्पाद में बदलने के लिए एक ऊर्जा अवरोध पार करना पड़ता है।
इसे निम्न उदाहरण द्वारा समझ सकते है –

(अभिकारक) AB + C → [A—–B—–C] → A + BC (उत्पाद)
इस वक्र से स्पष्ट है कि अभिकारक अणु सक्रियण ऊर्जा प्राप्त करके एक उच्च ऊर्जा वाली अस्थायी अवस्था बनाते है , इसे ही संक्रमण अवस्था कहते है।
यह संक्रमण अवस्था तुरंत टूटकर उत्पाद का निर्माण कर लेती है।
ऊष्माक्षेपी व ऊष्माशोषी अभिक्रियाओ के लिए वक्र :-
ऊष्मा क्षेपी के लिए –

ऊष्मा शोषी के लिए –

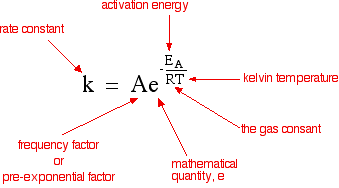
आरेनियस समीकरण (arrhenius equation in hindi) : आर्रेनियस नामक वैज्ञानिक ने सक्रियण ऊर्जा (Ea) व परम ताप T को वेग स्थिरांक K से सम्बन्धित करते हुए एक समीकरण दिया जो निम्न प्रकार है –
K = Ae-Ea/RT (समीकरण-1)
यहाँ K = वेग स्थिरांक
A = आर्रेनियस गुणांक
Ea = सक्रियण ऊर्जा
T = परम ताप
R = गैस स्थिरांक
समीकरण-1 आर्रेनियस समीकरण है।
समीकरण-1 को लघुगुणक के रूप में लिखने पर –
ln K = ln A – Ea/RT
इस समीकरण को log10 में परिवर्तित करने पर , (ln = 2.303 log)
2.303 log K = 2.303 log A – Ea/RT
इस समीकरण में 2.303 से भाग देने पर –
log K = log A – Ea/2.303RT (समीकरण-2)
समीकरण-2 Log के रूप में आर्रेनियस समीकरण है।
आरेनियस समीकरण से सक्रियण ऊर्जा (Ea) की गणना : इस समीकरण से सक्रियण ऊर्जा (Ea) की गणना दो प्रकार से कर सकते है।
- आरेखी विधि
- अन्तराल समीकरण से
- आरेखी विधि: इस विधि से log K व 1/t के मध्य वक्र द्वारा Ea ज्ञात कर सकते है।
समीकरण 2 से –
log K = -Ea/2.303RT + Log A (समीकरण-3)
समीकरण-3 की तुलना सरल रेखा समीकरण y = mx + c से करने पर –
y अक्ष पर = log K
x अक्ष पर = 1/T
ढाल = -Ea/2.303R
अन्त: खण्ड = log A
log K व 1/T के मध्य वक्र खीचने पर ये सरल रेखा के रूप में प्राप्त होता है –

ढाल = -Ea/2.303R
Ea = -2.303R x ढाल
इस सूत्र से सक्रियण ऊर्जा ज्ञात कर सकते है।
- अन्तराल समीकरण से: माना T1 व T2 ताप पर अभिक्रिया के वेग स्थिरांक क्रमशः K1 व K2 हो तो समीकरण 2 से –
Log K1 = – Ea/2.303RT1 + Log A (समीकरण-1)
Log K2 = -Ea/2.303RT2 + Log A (समीकरण-2)
समीकरण (2) में से समीकरण-1 घटाने पर और हल करने पर –
Ea = (log K2 – log K1)2.303RT1T2/(T2-T1) (समीकरण-3)
समीकरण-3 से सक्रियण ऊर्जा (Ea) ज्ञात कर सकते है।
प्रश्न 1 : निम्नलिखित वेग समीकरण के आधार पर अभिक्रिया वेग व वेग स्थिरांक की इकाई लिखिए।
यदि दाब को बार (bar) व समय को मिनट (minute) में मापा जाए तो
अभिक्रिया वेग = K (PCH3OCH3)3/2
उत्तर : अभिक्रिया वेग की इकाई = Bar min-1
अभिक्रिया वेग स्थिरांक K की इकाई = bar min-1/bar3/2
K = bar-1/2 min-1
प्रश्न 2 : परम ताप 298k में 10k की वृद्धि होने पर रासायनिक अभिक्रिया का वेग दुगुना हो जाता है। इस अभिक्रिया के लिए सक्रियण ऊर्जा की गणना कीजिये।
उत्तर : T1 = 298 k
T2 = 298 + 10 = 308 k
Ea = ?
R = 8.314 JK-1mol-1
K2/K1 = 2
Ea = (log K2 – log K1)2.303RT1T2/(T2-T1)
मान रखकर हल करने पर –
Ea = 52897 J/mol
प्रश्न 3 : हाइड्रो कार्बन का विघटन निम्न समीकरण के अनुसार होता है। Ea की गणना कीजिये।
K = (4.5 x 1011 S-1)e-28000/T
उत्तर : इस समीकरण की तुलना आरेनियस समीकरण K = Ae-Ea/RT से करने पर –
Ea/RT = 28000/T
Ea = 28000R
R = 8.314 JK-1mol-1
Ea = 232792 j/mol
प्रश्न 4 : H2O2 के प्रथम कोटि के विघटन को निम्न समीकरण द्वारा लिख सकते है –
Log K = 14.34 – 1.25 x 104 K/T
इस अभिक्रिया के लिए Ea की गणना कीजिये। कितने ताप पर इस अभिक्रिया की अर्द्धआयु 256 मिनट होगी ?
उत्तर : Log K = 14.34 – 1.25 x 104 K/T
समीकरण की तुलना आरेनियस की log समीकरण log K = log A – Ea/2.303RT से करने पर –
Ea/2.303RT = 1.25 x 104 K/T
Ea = 23.93 x 10-4 जूल/मोल
T ज्ञात करना है –
T1/2 = 256 मिनट = 15360 सेकंड
K1 = 0.693/t1/2
K1 = 45 x 10-6 sec-1
K1 का मान उपरोक्त समीकरण log K = log A – Ea/2.303RT में रखने पर और हल करने पर –
T = 669 K
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics