गुरुत्वीय त्वरण क्या है , परिभाषा , उदाहरण, सूत्र ,विमा , मात्रक , गुरुत्वाकर्षण g का मान (acceleration due to gravity in hindi)
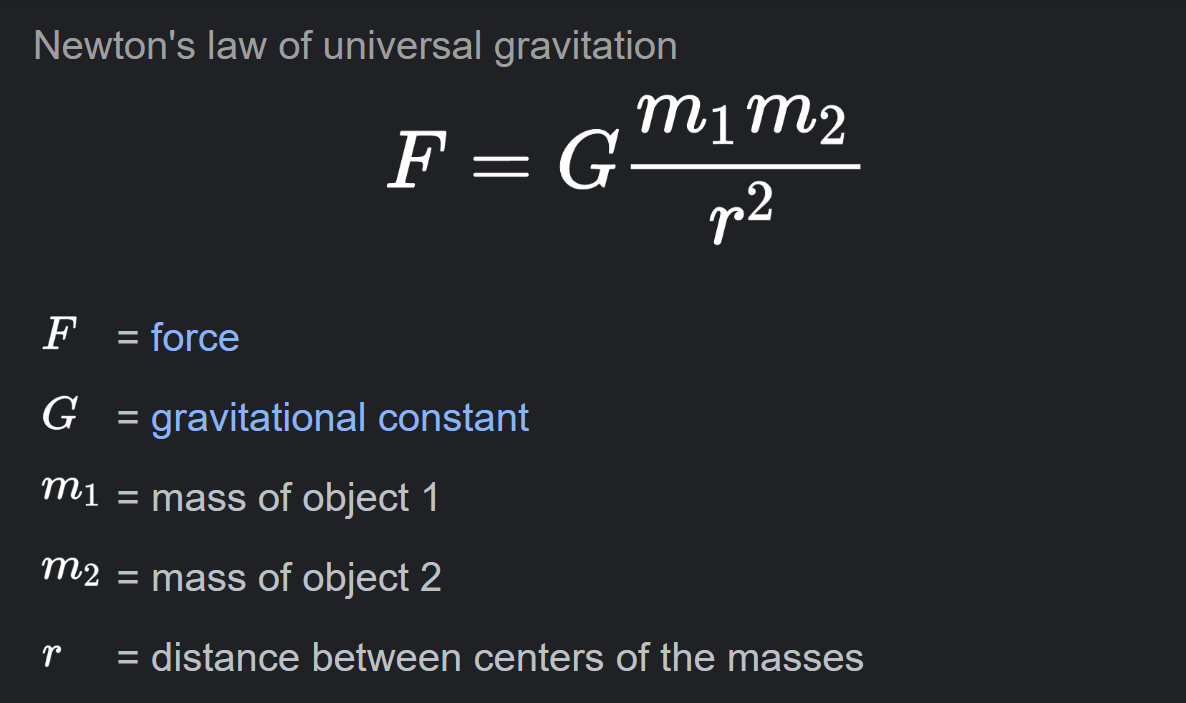
चूँकि जब किसी वस्तु पर बल लगाया जाता है तो वस्तु में त्वरण उत्पन्न हो जाता है , ऐसा हमने बल के अध्याय में अध्ययन किया था।
गुरुत्वीय त्वरण की परिभाषा : पृथ्वी आकर्षण बल के कारण प्रत्येक वस्तु पर आकर्षण बल लगाती है और इस बल की दिशा पृथ्वी के केन्द्र की तरफ होती है , पृथ्वी द्वारा प्रत्येक वस्तु पर आरोपित इस बल को गुरुत्वीय बल कहा जाता है।
न्यूटन के गति के दुसरे नियम के अनुसार जब किसी वस्तु पर बल कार्य करता है तो उसमे त्वरण (a = F/m) उत्पन्न हो जाता है।
अत: पृथ्वी के गुरुत्वीय बल के कारण वस्तु में भी एक त्वरण उत्पन्न हो जाता है इस गुरुत्व बल द्वारा उत्पन्न त्वरण को ही गुरुत्वीय त्वरण कहते है।
“गुरुत्व बल द्वारा किसी वस्तु में उत्पन्न त्वरण को गुरुत्वीय त्वरण कहा जाता है। ”
इसको ‘g’ द्वारा प्रदर्शित किया जाता है।
नोट : ध्यान दे कि G को सार्वत्रिक गुरुत्वाकर्षण नियतांक कहते है तथा g को गुरुत्वीय त्वरण कहा जाता है , कभी भी दोनों को एक ही राशी समझने की गलती न करे।
गुरुत्वाकर्षण त्वरण की संख्यात्मक मान 9.8 m/s² होता है।
गुरुत्वीय त्वरण के सूत्र की स्थापना
पृथ्वी का गुरुत्वीय त्वरण (acceleration due to gravity of the earth)
“सामान्यतया पृथ्वी द्वारा वस्तु पर आरोपित आकर्षी गुरुत्वीय बल को वस्तु का भार कहा जाता है। ” वस्तु के भार में उसके द्रव्यमान का भाग देकर गुरुत्वीय त्वरण प्राप्त किया जाता है। इसे सामान्यतया g से निरुपित किया जाता है।
पृथ्वी की सतह के निकट उपस्थित अन्य सभी गुरुत्वीय बल नगण्य माने जाते है , इसलिए हम भार को थी पृथ्वी के गुरुत्वाकर्षण के रूप में मानते है। चन्द्रमा की सतह पर , हम वस्तु के भार को चन्द्रमा के गुरुत्वाकर्षण के रूप में मानते है , क्योंकि यहाँ अन्य सभी गुरुत्वाकर्षण नगण्य होते है।
यदि हम पृथ्वी को M द्रव्यमान और R त्रिज्या की गोलीय सममित वस्तु माने तब पृथ्वी की सतह पर उपस्थित m द्रव्यमान की छोटी वस्तु का भार w
W = GMm/R2
या
mg0 = GMm/R2
जहाँ g0 = पृथ्वी की सतह पर गुरुत्वीय त्वरण
या
g0 = GM/R2 , यह पृथ्वी की सतह पर गुरुत्वीय त्वरण है।
स्पष्टत: g0 वस्तु के द्रव्यमान m से स्वतंत्र होती है। यह केवल पृथ्वी अथवा अन्य किसी ग्रह या उपग्रह , जिस पर भार लिया गया है , के द्रव्यमान M और त्रिज्या R पर निर्भर करता है।
g0 = GM/R2 से M = g0R2/G
इस सूत्र के प्रयोग से , केवेन्डिश ने पृथ्वी के M द्रव्यमान की गणना की , और उसने G = 6.67 x 10-11 N.m2/Kg2 का मापन किया। पृथ्वी का द्रव्यमान 5.98 x 1024 Kg प्राप्त हुआ।
नोट : यदि प्रश्न में समरूप पदार्थ परन्तु भिन्न भिन्न आकार की दो ठोस गोलीय वस्तुओं के लिए g के मान की तुलना करनी होगी , तब घनत्व और आयतन के गुणन द्वारा द्रव्यमान M प्रतिस्थापित करते है |
इस स्थिति में g = GM/R2 = Gp4πR3/3R2 = 4πGpR/3 और इसलिए g ∝ R
गुरुत्वीय त्वरण में परिवर्तन (variation in acceleration due to gravity)
गुरुत्वीय त्वरण (g) के मान को प्रभावित करने वाले तीन मुख्य कारक निम्नलिखित है –
- ऊँचाई
- गहराई
- अक्षांश और पृथ्वी का घूर्णन
- ऊंचाई के साथ गुरुत्वीय त्वरण (g) का परिवर्तन: पृथ्वी की सतह के ऊपर इसके केंद्र से r दूरी पर स्थित बिंदु पर , वस्तु का भार W = GMm/r2है।
या
g = GM/r2 , पृथ्वी की सतह के ऊपर इसके केंद्र से r दूरी पर गुरुत्वीय त्वरण |
या
g = GM/(r+h)2 , पृथ्वी की सतह से h ऊँचाई पर गुरुत्वीय त्वरण |
इसलिए g घटता है। चूँकि h बढ़ता है , अर्थात g = GM/R2(1 + h/R)2 = g0/(1+h/R)2 = g0(1+h/r)-2
यदि h << R , तब Gh = g0(1-2h/R) , [यदि h << R , तब h ऊँचाई पर गुरुत्वीय त्वरण]
यहाँ g0 पृथ्वी की सतह पर गुरुत्वीय त्वरण है |
नोट : आप इस अनुमानित सूत्र का उपयोग h = 400 km ऊँचाई तक कर सकते है। 400 किलोमीटर से कुछ कम ऊंचाई के लिए पुनः इस सूत्र का उपयोग करते है लेकिन निकटतम उत्तर को चिन्हित करते है।
- गहराई के साथ गुरुत्वीय त्वरण (g) का परिवर्तन (variation of g with depth): न्यूटन ने सिद्ध किया कि “पदार्थ का समरूप कोश इसके अन्दर स्थित कण पर गुरुत्वीय बल आरोपित नहीं करता है। “
चित्र M द्रव्यमान तथा R त्रिज्या की पृथ्वी को दर्शाता है। m द्रव्यमान की छोटी वस्तु को पृथ्वी के केंद्र O से r दूरी पर स्थित किया जाता है। यदि हम पृथ्वी को समरूप गोला (एक समान घनत्व) मानते है , तब पृथ्वी के साथ संकेन्द्रित r त्रिज्या के गोले का द्रव्यमान M’
M’ = [M/(4πR3/3)].4πr3/3 = Mr3/R3
न्यूटन के कोश सिद्धांत के अनुसार , m द्रव्यमान के बाहर d = R – r मोटाई का कोश इस द्रव्यमान पर कोई बल आरोपित नहीं करता है। इसलिए m द्रव्यमान पर गुरुत्वीय बल M’ (r त्रिज्या) द्रव्यमान के गोले के कारण बल है , जो कि आंतरिक द्रव्यमान है। इसलिए d गहराई पर इसका भार –
W = GM’m/r2 अथवा mg = GM’m/r2
अथवा g = GM’/r2
, पृथ्वी के केंद्र से r दूरी पर g
या g = GMr3/r2R3 = GMr/R3
अथवा g = kr , यहाँ K = GM/R3 वस्तु की किसी भी स्थिति के लिए पृथ्वी के लिए नियत है।
इस प्रकार g = GMr/R3 = kr , पृथ्वी के केंद्र से r दूरी g
इस प्रकार , पृथ्वी के अन्दर , g ∝ r लेकिन इसके बाहर g ∝ 1/r2 , अत: जब हम पृथ्वी की सतह से नीचे की ओर अथवा ऊपर की ओर जाते है , तब g का मान घटता है अर्थात पृथ्वी सतह पर g अधिकतम होता है।
इस प्रकार –
g = GMr/R3 = GM(R-d)/R3 = (GM/R2)(1-d/R)
या
Gd = g0(1-d/R) . . . . . . . [d गहराई पर गुरुत्वीय त्वरण]
यहाँ g0 = GM/R2 पृथ्वी की सतह पर g का मान है।
पृथ्वी के केंद्र पर d = R , इसलिए केन्द्र पर गुरुत्वीय त्वरण g = 0
नोट :
- गुरुत्वीय त्वरण (g ) के मान में कमी –
2g0h/R , पृथ्वी की सतह से ऊपर h << R ऊँचाई पर
g0d/R , पृथ्वी की सतह के निचे d गहराई पर
- यदि h , R की तुलना में है , तब सूत्र gh= g0(1-2h/R)का प्रयोग नहीं किया जायेगा। इस स्थिति में g = GM/(R+h)2 का प्रयोग किया जायेगा , जो कि h के सभी मानों के लिए वैद्य है , चाहे वह छोटा हो या बड़ा हो |
- समरूप गोलीय कोश के अन्दर गुरुत्वीय बल अर्थात भार और गुरुत्वीय त्वरण g शून्य होता है। इससे कोई फर्क नही पड़ता कि बिंदु द्रव्यमान कहाँ स्थित है। लेकिन यदि कोश असमरूप है , तब F , W और g अशून्य हो सकते है।
- ब्रह्माण्ड की प्रत्येक वस्तु अन्य वस्तु पर गुरुत्वीय बल आरोपित करती है , इससे कोई फर्क नहीं पड़ता कि वस्तु समरूप गोलीय कोश के अन्दर स्थित है या बाहर स्थित है। समरूप गोलीय कोश के अन्दर गुरुत्व केवल उस कोश के कारण ही शून्य होता है , कोश के बाहर (अथवा अन्दर) स्थित अन्य वस्तु के कारण शून्य नहीं होता है। इसलिए कोश , अपने अन्दर स्थित कण पर गुरुत्वीय बल आरोपित करके बाहर स्थित अन्य वस्तुओं को परिरक्षित नहीं करता है। इसलिए स्थिर विद्युत परिक्षण के विपरीत गुरुत्वीय परिरक्षण संभव नहीं होता है।
3. अक्षांश के साथ गुरुत्वीय त्वरण g का परिवर्तन और पृथ्वी का घूर्णन (variation of g with latitude rotation of the earth)
चित्र λ अक्षांश पर स्थित m द्रव्यमान के कण P को दर्शाता है , जो r = R cosλ त्रिज्या के वृत्त के अनुदिश w कोणीय वेग के साथ घूर्णन करेगा | यहाँ R पृथ्वी की त्रिज्या है |
यदि हम पृथ्वी के निर्देश तन्त्र में कार्य करते है , तब हम m द्रव्यमान के कण पर क्रियाशील mw2r छद्म बल (अपकेन्द्रीय बल) के अस्तित्व को मानते है |
इसलिए m पर इसकी साम्यावस्था में तीन बल क्रियाशील होते है –
- पृथ्वी के केंद्र की ओर (अर्थात उर्ध्वाधर नीचे की ओर) गुरुत्वीय बल mg
- CP के अनुदिश अपकेन्द्रीय बल mw2r
- अभिलम्ब बल (या m द्रव्यमान के गोलक के पेंडुलम की रस्सी में तनाव)
g’ = g – w2Rcos2λ
λ अक्षांश पर आभासी गुरुत्वीय त्वरण g |
चूँकि w2R = 3.37 x 10-2 ms-2 अत्यंत छोटा है और इसलिए (w2Rsinλcos λ)2 नगण्य होता है |
विषुवत पर : λ = 0 इसलिए g’ = g – w2Rcos2λ से g’ = g – w2R
या आभासी भार mg‘ = mg – mw2R
अर्थात
W’ = W – mw2R
विषुवत पर mw2R , mg के विपरीत है इसलिए परिणामी पृथ्वी के केंद्र की ओर है |
ध्रुवों पर λ = 90 डिग्री , इसलिए g’ = g – w2Rcos2λ से g’ = g
अर्थात ध्रुवो पर गुरुत्वीय त्वरण g में कोई आभासी परिवर्तन नहीं होता है |
इस प्रकार हम निष्कर्ष निकालते है कि पृथ्वी की घूर्णन गति के कारण भूमध्य पर आभासी g में कमी अधिकतम (= w2R = 0.0337 ms-2) होती है और ध्रुवों पर न्यूनतम (शून्य) होती है। दुसरे शब्दों में , आभासी भार ध्रुवों पर अधिकतम और भूमध्य पर न्यूनतम होता है।
नोट :
- यदि हमें पृथ्वी के घूर्णन का आवर्तकाल ज्ञात करना है ताकि विषुवत पर वस्तु भारहीनता अनुभव करे , तब g – w2R = 0याT = 2π/w = 2π/w = 2π√R/g = 84.6 मिनट , इसका अर्थ यह भी है कि पृथ्वी विषुवत पर वस्तु की भारहीनता के लिए इसकी वर्तमान घूर्णन चाल (24 घंटे/84.6 मिनट = 17) से 17 गुना चाल से घूर्णन करेगी।
- यदि पृथ्वी की कोणीय चाल बढती है , तब ध्रुवों के अतिरिक्त सभी स्थानों पर प्रभावी g का मान घटेगा।
- चूँकि पृथ्वी पश्चिम से पूर्व तक घूर्णन करती है , इसलिए हम अपने राकेटो को पश्चिम से पूर्व दिशा में प्रक्षेपित करते है ताकि राकेट पर प्रभावी g’ = g – w2R अल्प है।
- पृथ्वी की अगोलीयता: पृथ्वी एक पूर्ण गोला नहीं है। यह एक दीर्घवृत्तज है। भूमध्यीय तल में त्रिज्या ध्रुवों के अनुदिश त्रिज्या की अपेक्षा 21 किलोमीटर अधिक होती है। इसके कारण , गुरुत्व ध्रुवों पर अधिक होता है और भूमध्य पर कम होता है। ध्यान दीजिये कि भूमध्य पर घूर्णन और उभार दोनों के कारण गुरुत्वीय त्वरण का मान ध्रुवों की अपेक्षा भूमध्य पर कम होता है।
गुरूत्वीय त्वरण– जब कोई वस्तु ऊपर से मुक्त रूप से छोड़ी जाती है, तो वह गुरूत्व बल के कारण पृथ्वी की ओर गिरने लगती है और जैसे-जैसे वस्तु पृथ्वी के सतह के निकट आती जाती है, उसका वेग बढ़ता जाता है। अतः उसके वेग में त्वरण उत्पन्न हो जाता है। इसी त्वरण को गुरूत्वीय त्वरण कहते है। यदि किसी वस्तु का द्रव्यमान उ हो, तो इस पर कार्य करने वाला गुरूत्वीय बल उह (वस्तु का भार) के बराबर होगा। अतः गुरूत्वीय त्वरण उस बल के बराबर होता है, जिस बल से पृथ्वी एकांक द्रव्यमान वाली वस्तु को अपने केन्द्र की ओर आकर्षित करती है। यह वस्तु के रूप, आकार, द्रव्यमान इत्यादि पर निर्भर नहीं करता। इसे ह से प्रदर्शित करते है। इसका मात्रक ‘मीटर/सेकण्ड‘ अथ्वा ‘न्यूटर/किग्रा‘ है।
गुरूत्वजनित त्वरण ह का मान द्रवयमान पर निर्भर नहीं करता। अतः भिन्न-भिन्न द्रव्यमानों की दो वस्तुएँ मुक्त रूप से (वायु की अनुपस्थिति में) ऊपर से गिराई जायें, तो उसमें समान त्वरण उत्पन्न होगा। अर्थात समान ऊँचाई से एक साथ गिरने वाली वस्तु पृथ्वी पर एक ही साथ पहुंचेगी। वायु की उपस्थिति में वस्तु पर वायु का श्यानकर्षण तथा उत्प्लावन प्रभाव का प्रभाव पड़ता है। इस दशा में भारी वस्तुओं का त्वरण हल्के वस्तुओं की अपेक्षा अधिक होता है। इसी के कारण भारी वस्तु हल्के वस्तु की तुलना में पहले पृथ्वी पर पहुँचेगी।
गुरूत्वजनित त्वरण ‘ह‘ के मान में परिवर्तन 45° अक्षांश तथा समुद्र तल पर ह का प्रामाणिक मान 9.8 मीटर सेकण्ड होता है, अन्य स्थानों पर ह का मान थोड़ा-सा भिन्न होता है। पृथ्वी-तल पर ह का मान न्यूनतम भूमध्य रेखा पर, तथा अधिकतम ध्रुवों पर होता है।
– पृथ्वी-तल से ऊपर जाने पर ह का मान घटता है।
– पृथ्वी-तल के नीचे जाने पर भी ह का मान घटता है।
लिफ्ट मे व्यक्ति का भार- किसी लिफ्ट में व्यक्ति के भार में परिवर्तन निम्नलिखित प्रकार से होता है।
प्ण् जब लिफ्ट त्वरण ं से ऊपर जाती हैं, तो लिफ्ट में स्थित व्यक्ति का भार बढ़ा हुआ प्रतीत होता हैं।
प्प्ण् जब लिफ्ट त्वरण ं से नीचे आती हैं, तो इस दिशा में व्यक्ति का आभासी भार घटा हुआ प्रतीत होता हैं।
प्प्प्ण् जब लिफ्ट एकसमान वेग (त्वरण ं = 0) से ऊपर या नीचे जाती हैं, तो इस दशा में व्यक्ति को अपने भार में कोई परिवर्तन नहीं प्रतीत होता है।
प्टण् यदि नीचे आते वक्त लिफ्ट की डोरी टूट जाए, तो वह मुक्त वस्तु की भाँति नीचे गिरेगी। अतः ं त्र ह तथा ू = उह – उह = 0 अर्थात व्यक्ति को अपना भार शून्य प्रतीत होगा।
टण् यदि लिफ्ट के नीचे उतरते समय लिफ्ट का त्वरण गुरूत्वीय त्वरण से अधिक हो (अर्थात ं झ ह) तो लिफ्ट में खड़ा व्यक्ति लिफ्ट की फर्श से उठकर उसकी छत पर जा लगेगा।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics