उदाहरण : किसी वाहन में लगे पहिये की गति घूर्णन गति होती है क्यूंकि यह अपनी अक्ष के चारों तरफ गति करता है और एक निश्चित समान समयांतराल में पहिये के सभी कण समान कोणीय विस्थापित होते है।
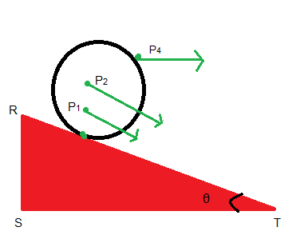
चित्रानुसार जब एक गोलाकार आकृति को झुकी हुई सतह से छोड़ा जाता है तो यह घूमता हुआ आगे की तरफ बढ़ता है अर्थात यह घूर्णन भी करता है और आगे की तरफ भी अपनी स्थिति परिवर्तित करता है अर्थात गति करता है।
अत: यहाँ दो प्रकार की गति हो रही है –
1. आकृति अपनी अक्ष पर घूम रही है अर्थात घूर्णन गति हो रही है।
2. वस्तु आगे की तरफ समय के साथ अपनी स्थिति परिवर्तित कर रही है अत: यहाँ स्थानान्तरीय गति भी हो रही है।
अब निश्चित रूप से आप स्थानान्तरीय गति और घूर्णन गति में अन्तर को समझ गए होंगे।
चूँकि घूर्णन गति में वस्तु के सभी कण एक वृत्तीय पथ का अनुसरण करते है तथा इन सभी वृत्तीय पथों के केंद्र को मिलाने वाली रेखा को घूर्णन की अक्ष कहा जाता है।
चूँकि घूर्णन गति में वस्तु या पिण्ड के सभी कणों का एक समय अन्तराल में समान कोणीय विस्थापन होता है अत: हम कह सकते है कि वस्तु के सभी कण एक समान कोणीय वेग से गति करते है लेकिन इन कणों का रेखीय वेग अलग अलग होता है। जो बिंदु अक्ष पर स्थित होते है उनका रेखीय वेग का मान शून्य होता है।
किसी भी क्षण पर वस्तु की स्थिति को प्रदर्शित करने के लिए तीन चरों का प्रयोग किया जाता है अत: घूर्णन गति के लिए स्वतंत्रता की कोटि का मान 3 होता है।
घूर्णन गति (Rotational motion) : यदि कोई पिण्ड या निकाय किसी स्थिर अक्ष के परित: इस प्रकार गति करता है कि उसके सभी कण वृत्तिय पथों पर चलते है ताकि एक निश्चित समयांतराल में प्रत्येक कण का कोणीय विस्थापन समान हो तो उसकी गति को घूर्णन गति कहते है।
इस समस्त वृत्तीय पथो के केन्द्रों को मिलाने वाली रेखा को घूर्णन अक्ष कहते है।
पिंड के सभी कणों के कोणीय वेग समान होते है लेकिन उनके रेखीय वेग (v = rw) अलग अलग होते है। अक्ष पर स्थित बिन्दुओं के लिए रेखीय वेग शून्य होते है। किसी क्षण पर पिंड के अभिविन्यास को तीन चरों , जिन्हें घूर्णन स्वतंत्रता की कोटियाँ कहते है , से व्यक्त किया जा सकता है।
शुद्ध घूर्णन गति
चित्र में किसी भी आकार का एक दृढ़ पिंड एक स्थिर घूर्णन अक्ष के परित: घूर्णन कर रहा है। पिंड का प्रत्येक बिंदु एक वृत्त में घूमता है , जिसका केंद्र घूर्णन अक्ष पर है और प्रत्येक बिंदु किसी समय अंतराल में समान कोण घूमता है , ऐसी गति को शुद्ध घूर्णन गति कहते है। चूँकि पिण्ड दृढ है , अत: प्रत्येक कण का कोणीय वेग समान है।
v1 = wr1 , v2 = wr2 ,v3 = wr3 . . . . .. vn = wrn
कुल गतिज ऊर्जा = m1v12/2 + m2v22/2 + . . . . .
= [m1r12 + m2r22 + . . . . .. ]w2/2
= Iw2/2
यहाँ I = m1r12 + m2r22 + . . . . .. (जडत्व आघूर्ण है। )
w = पिण्ड का कोणीय वेग
सम्मिलित स्थानांतरीय गति
एक पिण्ड सम्मिलित स्थानांतरीय गति और घूर्णन गति करता है , यदि पिण्ड के सभी बिंदु किसी अक्ष के परित: घुमे और वह अक्ष स्वयं भूमि के सापेक्ष स्थानांतरीय गति करे। किसी दृढ़ पिंड की सामान्य गति को एक सम्मिलित स्थानांतरीय गति और घूर्णन गति के रूप में देखा जा सकता है।
रेखीय गति और घूर्णन गति के समीकरण :-
रेखीय गति :-
(i) यदि त्वरण शून्य हो तब v = नियतांक s = vt
(ii) यदि त्वरण a = नियतांक हो तो ,
(i) s = (u+v)t/2
(ii) a = v-u/t
(iii) v = u + at
(iv) s = ut + at2/2
(v) v2 = u2 + 2as
(vi) Snth = u + a(2n-1)/2
(vii)यदि त्वरण a = नियतांक नहीं हो तो उपरोक्त समीकरण प्रयुक्त नहीं होती है। तब
(i) v = dx/dt
(ii) a = dv/dt = dx2/dt2
(iii) vdv = ads
घूर्णन गति के समीकरण :-
(i) यदि कोणीय त्वरण शून्य हो तो w = नियतांक , ʘ = wt
(ii) यदि कोणीय त्वरण नियतांक हो तो –
(a) ʘ = (w1 + w2)t/2
(b) ά = w2-w1/t
(iii) w2 = w1 + άt
(iv) ʘ = w1t + άt2/2
(v ) ʘ w12 + 2άʘ
(vi) ʘnth = w1 + (2n-1)ά/2
(iii) यदि कोणीय त्वरण नियतांक नहीं हो तो उपरोक्त समीकरण प्रयुक्त नहीं होती है तब –
(i) w = dθ/dt
(ii) α = dw/dt = d2θ/dt2
(iii) wdw = αdθ
एक दृढ़ पिण्ड की सम्मिलित स्थानान्तरण तथा घूर्णन गति : दृढ पिंड की व्यापक गति दो स्वतंत्र गतियो के योग रूप में समझी जा सकती है। एक तो पिण्ड के किसी बिंदु की स्थानांतरित गति और दूसरी इस बिंदु के सापेक्ष पिंड की घूर्णन गति।
पिण्ड का द्रव्यमान केंद्र इस बिंदु के लिए चयन करना सुविधाजनक रहता है , चूँकि इससे गणितीय गणनाएँ स्वीकृत हो जाएगी।
एक रेल में एक पंखे को , प्लेटफार्म पर खड़ा प्रेक्षक A देखता है।
यदि पंखा बंद है जबकि रेल चल रही है तो पंखे की गति शुद्ध स्थानान्तरीय होगी , चूँकि पंखे का प्रत्येक बिंदु समान समय में समान दूरी विस्थापित हो रहा है।
यदि पंखा चालू (शुरू) करे जबकि रेल खड़ी है तो पंखे की गति अंश के सापेक्ष शुद्ध घूर्णन गति है , चूँकि अक्ष पर स्थित सभी बिंदु स्थिर है जबकि अन्य सभी बिंदु अक्ष के सापेक्ष समान कोणीय वेग से घूम रहे है।
यदि चलती रेल में पंखा चालु (शुरू) किया जाए तो प्लेटफार्म पर स्थित प्रेक्षक के लिए पंखे की गति न तो शुद्ध स्थानान्तरीय है और न ही शुद्ध घूर्णन गति है।
इस प्रकार की गति दृढ पिण्ड की व्यापक गति का अच्छा उदाहरण है।
अब यदि प्रेक्षक B रेल में ही स्थित है तो उसे पंखे की गति शुद्ध घूर्णन गति और B की (A के सापेक्ष) शुद्ध स्थानांतरीय गति के योग रूप में विघटित की जा सकती है।
इस प्रकार दृढ़ पिण्ड की व्यापक गति का शुद्ध घूर्णन और शुद्ध स्थानान्तरण गति के विघटन सिर्फ रेल में स्थित पंखे के लिए ही नहीं , अपितु किसी भी दृढ पिण्ड की गति के लिए सही (सटीक) है।
दृढ पिण्ड की व्यापक गति की गतिकी
पूर्व कथन के अनुसार किसी भी दृढ़ पिण्ड के किसी भी बिन्दु का इसी पिंड के किसी भी अन्य बिंदु के सापेक्ष कोणीय विस्थापन (θ) , कोणीय वेग (w) , कोणीय त्वरण (α) समान होता है।
अत: यदि हम पिण्ड के किसी बिंदु (माना A) का वेग और किसी भी बिन्दु का अन्य किसी भी बिन्दु के सापेक्ष कोणीय वेग (माना w) जानते है तो इस दृढ़ पिण्ड पर स्थित किसी भी बिंदु का वेग परिकलित किया जा सकता है | चूँकि दूरी AB नियत है |
चूँकि दूरी AB नियत है –
VBA ⊥ AB
ज्ञातव्य है कि w = VBA⊥/rBA
VBA⊥ = VBA = wrBA
सापेक्ष वेग सूत्र से : VBA = VB – VA
VB = VA + VBA
VB = VA + w x rBA
इसी प्रकार aB = aA + α x rBA [किसी भी दृढ़ पिण्ड निकाय के लिए]
घूर्णन की तात्क्षणिक अक्ष
यह वह अक्ष है जिसके सापेक्ष सम्मिलित स्थानान्तरण तथा घूर्णन गति , शुद्ध घूर्णन गति प्रतीत होती है।
द्रव्यमान केंद्र के स्थानान्तरण तथा घूर्णन का सम्मिलित प्रभाव , द्रव्यमान केन्द्र से पारित अक्ष के सापेक्ष , समान कोणीय चाल से किसी स्थिर अक्ष के सापेक्ष शुद्ध घूर्णन के समान होगा। ये अक्ष घूर्णन की तात्क्षणिक अक्ष कहलाती है। ये किसी एक क्षण के लिए परिभाषित है और इसकी स्थिति समय के साथ बदलती है।
उदाहरण : शुद्ध लोटनी गति में सतह के साथ सम्पर्क बिंदु घूर्णन की तात्क्षणिक अक्ष कहलाती है।
घूर्णन की तात्क्षणिक अक्ष का ज्यामितीय निर्माण (I.A.R) : दृढ़ पिण्ड पर स्थित दो बिन्दुओं पर वेग सदिश खींचो। घूर्णन की तात्क्षणिक अक्ष उन बिन्दुओं पर डाले गए लम्ब का मिलान बिंदु है।
शुद्ध लोटनी गति की स्थिति में तात्क्षणिक अक्ष निम्न बिंदु घूर्णन की तात्क्षणिक अक्ष है।
शुद्ध लोटनी गति में वस्तु की गति की इस अक्ष के सापेक्ष शुद्ध घूर्णन गति के रूप में भी व्याख्या कर सकते है।
τP = IPα
LP = IPw
गतिज ऊर्जा (K.E.) = IPw2/2
यहाँ IP घूर्णन की तात्क्षणिक अक्ष जो P से पारित है के सापेक्ष जडत्व आघूर्ण है।
नोट : एक समान वस्तु की शुद्ध लोटनी गति में बलाघूर्ण की समीकरण को भी सम्पर्क बिंदु के सापेक्ष लागू किया जा सकता है।