Syndrome calculator , syndrome calculation in cyclic codes , cyclic encoder design
cyclic encoder design , Syndrome calculator , syndrome calculation in cyclic codes , cyclic encoder design , design of encoder and syndrome calculator for cyclic codes :-
EXAMPLE 10.37. Determine the encoded message for the following 8 bit data codes using the following CRC generating polynomial :
P(x) = x4 + x3 + x0
(i) 1 1 0 0 1 1 0 0
(ii) 0 1 0 1 1 1 1 1
Solution : The given message is 1 1 0 0 1 1 0 0. This means that there are 8 message bits.
Thus, k = 8
We know that the degree of generator polynomial is equal to the number of parity (check) bits in the code.
Therefore, number of parity bits (n – k) = 4
Hence, codeword length, n = 8 + 4 = 12
Hence the message polynomial corresponding to the message 1 1 0 0 1 1 0 0 is given as
M(x) = x7 + x6 + 0x + 0x4 + x3 + x2 + 0x +0
or M(x) = x7 + x6 + x2 + x2
Now, the generator polynomial is given by,
P(x) = x4 + x3 + 1
Next, let us multiply the message polynomial by xn-k i.e. x4
Thus, x4 [M(x)] = x4 [x7 + x6 + x3 + x2]
or x4 M(x) = x11 + x10 + x7 + x6
let us divide x4 M(x) by the generator polynomial as under :
equation
Mod 2 addition →
Mod 2 addition →
Mod 2 addition →
Mod 2 addition →
Now, let us obtain the codeword polynomial X(x) as under :
X(x) = x4 M(x) + C(x)
or X(x) = (x11 + x10 + x7 + x6) + (x3 + x2 + x + 1)
or X(x) = x11 + x10 + 0x9 + 0x8 +x7 + x6 + 0x5 + 0x4 + x3 + x2 + x +1
Hence, the codeword will be
equation
(ii) Similarly, we can obtain the codeword for the other message. The corresponding codeword for the message 0101111 is,
equation
EXAMPLE 10.38. Using the generator polynomial g(x) = 1 + x2 + x3, generate the systematic and non systematic cyclic codewords for the message vectors 1011 and 1001.
Solution : Non systematic code vectors
The number of message bits = k = 4
Therefore, the number of parity bits (n – k) = degree of generator polynomial = 3
The total number of hits per codeword n = 4 + 3 + 7
The message polynomial for the message vector 1011 is given by
M(x) = m0 + m1x + m2x2 + m3x3 …(i)
Substituting the value of m0 ….., m3 we obtain
M(x) = 1 + x2 + x3 …(ii)
Therefore, the generator polynomial is given by,
g(x) = 1 + x2 + x3
Also, the non systematic cyclic codeword polynomial is given by :
X(x) = M(x) . g(x) = (1 + x2 + x3) (1 + x2 + x3)
or X(x) = 1 + x2 + x3 + x2 + x4 + x5 + x3 + x5 + x6
or X(x) = 1 + x2 (1 + 1) + x3 (1 + 1) + x4 + x5 (1 + 1) + x6
But. 1 + 1 = 0 (Modulo-2 addition).
so, X(x) = 1 + x4 + x6
It may be noted that the degree of the codeword polynomial is 6 i.e. (n – 1). The codeword is given by,
X = (1 0 0 0 1 1 1) Ans.
This is the non systematic codeword for the message vector 1011.
Systematic code vector
Let us multiply M(x) by xn-k as under:
xn-k M(x) = x3 [1 + x2 + x3] = x3 + x5 + x6
Now, we divide xn-k M(x) by the generator polynomial.
The division is as under :
equation
Next, let us obtain the codeword polynomial X(x).
The codeword polynomial can be obtained by adding Dn-k M(p) to the remainder polynomial C(x).
Thus X(x) = [xn-k M(x)] Å C(x)]
or X(x) = x6 + x5 + 0x4 + x3 + 0x2 + 0x + 0] Å [0 + 0 + 0]
or X(x) = [0 + 0x + 0x2 + x3 + 0x4 + x5 + x6]
Hence, the codeword is given by,
diagram
EXAMPLE 10.39. Sketch the encoder and syndrome calculator for the generator polynomial g(x) = 1 + x2 + x3, and obtain the syndrome for the received codeword 1001011.
Solution : Encoder :
The received code word has 7 bits, hence, n = 7 and the degree of generator polynomial is 3, hence, n – k = 3, so k = 4. Thus, the given code is a (7, 4) cyclic code.
The generator polynomial of an (n, k) cyclic code is expressed as,
equation
or equation
The given generator polynomial is,
g(x) = 1 + 0x + x2 + x1 …(ii)
Comparing equations (i) and (ii), we obtain
g1 = 0, g2 = 1
Hence, the encoder is shown in figure 10.45.
diagram
FIGURE 10.45 Encoder for example 10.38.
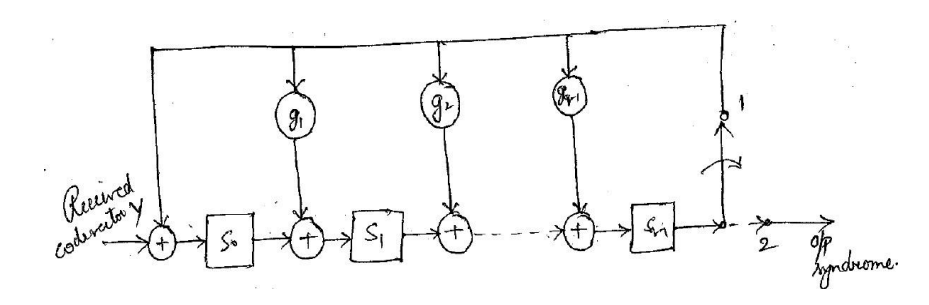
Syndrome calculator
The given generator polynomial is,
g(x) = 1 + x2 + x3
or g(x) = x3 + x2 + 0x + 1 …(iii)
We know that the general form of generator polynomial is given by
g(x) = x3 + g2x2 + g1x + 1 …(iv)
Comparing equations (iii) and (iv), we get
g1 = 0
g2 = 1
The syndrome calculator is shown in figure 10.46.
diagram
FIGURE 10.46. Syndrome calculator.
Calculation of syndrome
The output switch of figure 10.46 will be initially in position 1 until all the 7 bits of the received signal Y are shifted into the register. After that, the output switch is shifted to position 2. Clock pulses are then applied to the shift register to output the syndrome vector S. Table 10.16 explains the process of syndrome generation.
Thus, the required syndrome will be
S = 100
Table 10.16.
| Shift | Input bits (Y) |
Contents of the shift register | ||
| S0 = Y Å S2 | S1 = S0 | S2 = S1 Å S0 | ||
| — | 0 | 0 | 0 | |
| 1 | 1 (LSB) | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 1 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 1 | 1 | 1 |
| 5 | 0 | 1 | 1 | 0 |
| 6 | 0 | 0 | 1 | 1 |
| 7 | 1 (MSB) | 0 | 0 | 1 |
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics