Ln(x) रोड्रिज सूत्र क्या है समझाइये | RODRIGUE FORMULA FOR Ln(x) in hindi definition
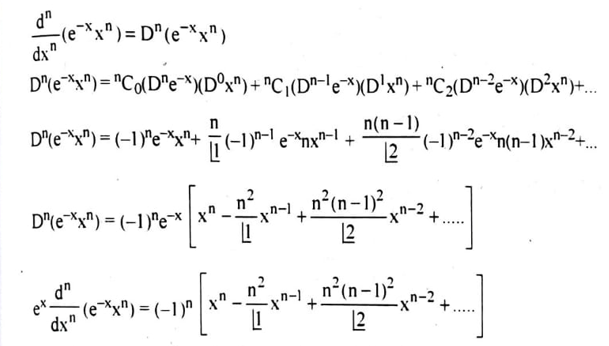
RODRIGUE FORMULA FOR Ln(x) in hindi definition Ln(x) रोड्रिज सूत्र क्या है समझाइये ?
Ln(x) रोड्रिज सूत्र (RODRIGUE FORMULA FOR Ln(x))
लागेर बहुपद को निम्न रोड्रिज सूत्र द्वारा भी ज्ञात कर सकते हैं।
दो फलनों के गुणन के अवकलजों के लिये लिबनीज सूत्र (Leibniz formula) का उपयोग करने पर,
इस समीकरण का दायाँ पक्ष n कोटि के लगेर बहुपद की श्रेणी है इसलिये
इस रोड्रिज सूत्र से विभिन्न कोटि के लागेर बहुपद ज्ञात कर सकते हैं।
प्रथम तन कोटि के लागेर बहुपदों का ग्राफीय निरूपण चित्र (7.23-1) में दर्शाया गया है।
लागेर फलनों का लाम्बिकता सम्बन्ध (ORTHOGONALITY RELATION FOR LAGUERRE FUNCTION)
लागेर बहुपद स्वयं लाम्बिकता समुच्चय (set ) नहीं बनाते हैं तथापि Ln (x) का एक फलन शून्य व के बीच लाम्बिकता समुच्चय बनाता है।
परिस्थिति – I : जब m = n
लागेर समीकरण से,
इसे e-x से गुणा करने पर,
इस समीकरण में n को m से बदलने पर,
समीकरण (1) को Lm(x) से तथा समीकरण (2) को Ln(x) से गुणा कर फिर घटाने पर,
इस समीकरण का 0 से 0 के बीच x के सापेक्ष समाकलन करने पर,
परिस्थिति – II : जब m=n
लागेर बहुपद के घात श्रेणी
तथा रोड्रिज सूत्र से,
इस समीकरण के दायें पक्ष के समाकल को खण्डश समाकलन n बार करते हैं।
इस समीकरण के दायें पक्ष का प्रथम पद शून्य के बराबर होता है अतएव
इस प्रक्रम को बार-बार करने से निम्न परिणाम प्राप्त होता है।
इन समाकलनों को समीकरण (4) में रखने पर,
समीकरण (3) व (6) को एक समीकरण के रूप में लिखने पर,
अतः फलन लाम्बिकता गुण को दर्शाता है।
सह लागेर समीकरण (ASSOCIATED LAGUERRE POLYNOMIAL)
सह-लागेर अवकल समीकरण लेबनिट्ज प्रमेय (Leibnitz theorem) की सहायता से लागेर अवकल समीकरण को m बार अवकलित करके प्राप्त किया जा सकता है। लेबनिट्ज प्रमेय के कथन के अनुसार
लागेर अवकल समीकरण से,
इस प्रमेय का उपयोग करके लागेर समीकरण को m बार अवकलित करके तथा kth अवकलज को (dk / dxk) = Dk लिखने पर,
यह समीकरण सह लागेर समीकरण कहलाता है।
चूँकि y(x) = Ln(x) लागेर समीकरण का हल है इसलिये सह लागेर समीकरण के हल को लिख सकते हैं।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics