Relativistic Electrodynamics in hindi आपेक्षिकीय विद्युतगतिकी नोट्स क्या है परिभाषा
आपेक्षिकीय विद्युतगतिकी नोट्स क्या है परिभाषा Relativistic Electrodynamics in hindi ?
अध्याय : आपेक्षिकीय विद्युतगतिकी (Relativistic Electrodynamics)
आवेश के संरक्षण का नियम तथा सांतत्य समीकरण (LAW OF CONSERVATION OF CHARGE AND EQUATION OF CONTINUITY)
आवेश के संरक्षण के नियमानुसार आवेश को न तो उत्पन्न किया जा सकता है और न ही समाप्त किया जा सकता है। अतः विलगित निकाय का कुल आवेश अर्थात् ऋणात्मक तथा धनात्मक आवेश का बीजगणितीय योग, सदैव नियत रहता है। अतः दूसरे शब्दों में हम कह सकते हैं कि किसी पृष्ठ से बद्ध आयतन में से आवेश के कमी की दर उसी आयतन में से निर्गत धारा के बराबर होती है। इस कथन को गणितीय रूप से सांतत्य समीकरण के द्वारा प्रदर्शित कर सकते हैं।
किसी पृष्ठ द्वारा बंद आयतन में आवेश की कमी की दर को सामान्यतया धारा (current) द्वारा परिभाषित करते हैं, अत: धारा
जहाँ q बंद आयतन में आवेश की मात्रा है।
यदि किसी बंद आयतन के एकांक पृष्ठ से J धारा निर्गत हो रही है जहाँ J को धारा घनत्व (current density) से परिभाषित करते हैं तो सम्पूर्ण पृष्ठ से निर्गत कुल धारा
इसी प्रकार बंद आयतन में आवेश प्रति एकांक आयतन को आवेश घनत्व (charge density) से परिभाषित करते हैं, इसलिये बंद आयतन में कुल आवेश
समीकरण (2) तथा (3) को समीकरण (1) में रखने पर,
गॉस डाइवर्जेन्स प्रमेय (Gauss divergence theorem) का उपयोग करने पर,
चूँकि यह समाकलन सभी आयतन के लिए वैध है। अतः
इस समीकरण को सांतत्य समीकरण कहते हैं। इस समीकरण को प्रदिश संकेतों में भी लिख सकते हैं।
समीकरण (4) को घटकों में लिखने पर,
प्रदिश संकेतन पद्धति में लिखने पर,
आंसटीन संकलन परिपाटी (Einstein summation convention) का उपयोग करने पर,
जहाँ Ju को चतुर्विम धारा घनत्व सदिश (four-current vector) तथा को चतुर्विम डाइवर्जेन्स संकारक (divergence operator) कहते हैं। समीकरण (5) सांतत्य समीकरण का सहप्रसरण रूप कहलाता है।
आवेश तथा धारा घनत्वों का लॉरेंज रूपान्तरण (LORENTZ TRANSFORMATION OF CHARGE AND CURRENT DENSITIES)
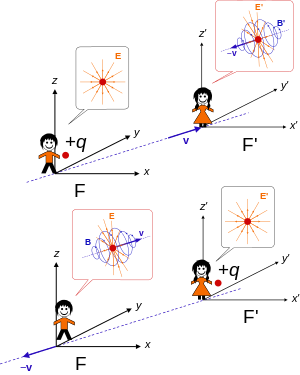
आपेक्षिकीय विद्युतगतिकी में धारा घनत्व तथा आवेश घनत्व को पृथक नहीं माना गया है इसका कारण है कि यदि आवेश एक जड़त्वीय निर्देश तंत्र में स्थिर है तो वह दूसरे जड़त्वीय निर्देश तंत्र में, जो नियत वेग से पहले निर्देश तंत्र के सापेक्ष गतिशील है, में धारा की भांति व्यवहार करता है इसलिये चतुर्विम आकाश में आवेश तथा धारा घनत्व दोनों मिलकर एक चतुर्विम सदिश बनाते हैं जिसे Ju से व्यक्त किया जाता है। पिछले खण्ड में धारा घनत्व चतुर्थ घटक J4 = icp को परिभाषित किया था। अतः चतुर्विम धारा घनत्व सदिश को घटकों में निम्न रूप में लिख सकते हैं
Ju = (J, icp) …(1)
यह सिद्ध करने के लिए, कि Ju चतुर्विम धारा घनत्व का चतुर्थ घटक होता है माना आवेश dq को एक अल्पांश आयतन dx1 dx2, dx3 में लेते हैं जिसमें आवेश घनत्व है।
dq=pdx1 dx2 dx3
उपरोक्त समीकरण के दोनों तरफ dxu से गुणा करने पर,
चूँकि आवेश dq तथा dxu दोनों लॉरेंज निश्चर (invariant) होते हैं इसलिये समीकरण ( 2 ) का RHS भी लॉरेंज निश्चर होगा।
Ju के लॉरेंज निश्चर तथा इसके चार घटक होने के कारण ही इसे चतुर्विम-धारा घनत्व कहा जाता है। हम जानते हैं कि यदि कोई चतुर्विम- सदिश A लॉरेंज निश्चर हो तो उसे एक जड़त्वीय निर्देश तंत्र से दूसरे निर्देश तंत्र में निम्न सम्बन्ध द्वारा रूपान्तरित कर सकते हैं।
चूँकि चतुर्विम-धारा घनत्व एक सदिश राशि तथा लॉरेंज निश्चर है इसलिये इसे सम्बन्ध (5) की भांति लिख सकते हैं।
समीमरण (5) को घटकों में लिखने पर,
समीकरण (7a) तथा (7d) में चतुर्थ घटक को आवेश घनत्व के रूप में लिखने पर,
समीकरण (7b), (7c), (8) तथा ( 9 ) धारा तथा आवेश घनत्वों के लॉरेंज रूपान्तरण समीकरण कहलाते हैं।
विशिष्ट स्थिति :
(i) यदि स्थिर निर्देश तंत्र में आवेश वितरण नियत है तो J1 = J2 = J3 = 0. लॉरेंज रूपान्तरण समीकरण (7b), (7c), (8) तथा (9) से,
(ii) माना एक जड़त्वीय निर्देश तंत्र S में एक आयतन अल्पांश dx1 dx2 dx3 है जिसमें नियत आवेश घनत्व p है। अतः इस आयतन अल्पांश में कुल आवेश,
dq= pdx1 dx2 dx3
दूसरे निर्देश तंत्र S’ जो निर्देश तंत्र S के सापेक्ष + X – अक्ष के अनुदिश नियत वेग vगतिशील है, में उसी आवेश का आयतन अल्पांश dx1 dx2 dx3 में आवेश घनत्व p है तो
अतः आवेश की मात्रा लॉरेंज रूपान्तरण में निश्चर रहती है जबकि आवेश घनत्व निश्चर नहीं रहता है।
विद्युतचुम्बकीय विभव (ELECTROMAGNETIC POTENTIAL) विद्युत आवेश एक क्षेत्र के स्रोत होते हैं जिसमें स्थिर अन्य आवेश विद्युत बल अनुभव करता है। इस क्षेत्र को विद्युत क्षेत्र कहते हैं। किसी आवेश द्वारा उत्पन्न विद्युत क्षेत्र को एक अन्य राशि $ से सम्बन्धित कर सकते हैं जो विद्युत क्षेत्र की तीव्रता के ऋणात्मक प्रवणता के बराबर होता है। अतः …………….(1)
एक अदिश राशि होती है जो आवेश से प्रेक्षक बिन्दु की दूरी पर निर्भर करती है तथा विद्युत क्षेत्र द्वारा किये गये कार्य का मापन करते है, इसे अदिश विभव या विद्युत विभव कहते हैं । चूँकि किसी अदिश राशि के प्रवणता का कर्ल सदैव शून्य के बराबर होता है अतः उपरोक्त समीकरण से,
जो स्थिर विद्युत क्षेत्र के संरक्षित प्रकृति को व्यक्त करता है । जब आवेश गति करता है तो यह धारा को उत्पन्न करता है जो एक अन्य क्षेत्र का स्रोत होता है। इसे चुम्बकीय क्षेत्र कहते हैं। हम चुम्बकीय क्षेत्र B को एक अन्य भौतिक राशि विभव द्वारा हैं परन्तु यह विभव चुम्बकीय क्षेत्र के गॉस समीकरण B = 0 द्वारा निर्धारित होता व्यक्त कर सकते है। चूँकि किसी सदिश के कर्ल का डाइवर्जेंस भी सदैव शून्य के बराबर होता है। अतः चुम्बकीय क्षेत्र B को एक भौतिक राशि से सम्बन्धित करते हैं जो निम्न समीकरण द्वारा प्राप्त होता है और इसे चुम्बकीय सदिश विभव कहते अतः
अब यदि विद्युत क्षेत्र तथा चुम्बकीय क्षेत्र समय पर निर्भर करते हैं तो दोनों क्षेत्र E व B मैक्सेवल के समीकरणों द्वारा युग्मित हो जाते हैं। मैक्सवेल के समीकरण से, v×Ē= ав इसमें समीकरण ( 2 ) रखने पर,
चूँकि किसी अदिश राशि के प्रवणता का कर्ल सदैव शून्य के बराबर होता है इसलिये
को किसी अदिश राशि के प्रवणता के रूप में लिखा जा सकता है। अतः
अतः E तथा B को ज्ञात करने के लिए पहले विद्युत विभव तथा चुम्बकीय विभव A को ज्ञात करना होगा। A तथा को ज्ञात करने के लिए मैक्सवेल के एक अन्य समीकरण का उपयोग करते हैं।
जहाँ j धारा घनत्व है तथा u0 एवं Eo मुक्त आकाश की क्रमशः चुम्बकशीलता तथा विद्युतशीलता है। इसमें समीकरण (2) व (3) रखने पर,
समीकरण (5) व (7) विद्युत चुम्बकीय विभव Āव के असमांगी युग्मित तरंग समीकरण है।
चूँकि A व स्वैच्छिक विभव हैं इसलिये इनके मान इस प्रकार लिये जाते हैं कि ये निम्न प्रतिबंध की शर्त को पूरा करें। A व ¢ पर लगाये गये प्रतिबंध को लॉरेंज प्रतिबंध (Lorentz condition) कहते हैं।
लॉरेंज प्रतिबंध (8) का समीकरण (5) व (7) में उपयोग करने पर इन समीकरणों को अयुग्मित कर देती है। तथा
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics