ORTHOGONALITY RELATION OF LEGENDRE POLYNOMIALS in hindi लिजेंड्रे बहुपदों में लाम्बिक सम्बन्ध

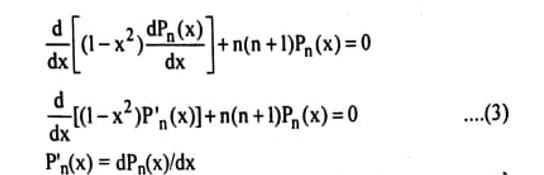
लिजेंड्रे बहुपदों में लाम्बिक सम्बन्ध ORTHOGONALITY RELATION OF LEGENDRE POLYNOMIALS in hindi ?

लेजेंड्रे बहुपदों में लाम्बिकता सम्बन्ध (ORTHOGONALITY RELATION OF LEGENDRE POLYNOMIALS) 

लेजेंड्रे फलन ऐसे फलन होते हैं जो ट्रिगोनोमिट्रिक (trignonometric) फलनों की भांति लाम्बिकता गुण को दर्शाते हैं। गणितीय रूप से इस गुण को निम्न समाकल द्वारा दर्शाते हैं।

चूँकि लेजेंड्रे बहुपद Pn (x) लेजेंड्रे अवकल समीकरण का हल हैं इसलिये अवकल समीकरण में Pn(x) का उपयोग करते हैं।

समीकरण (3) को Pm(x) से गुणा कर तथा 1 से 1 के बीच x के सापेक्ष समाकलन करने

प्रथम पद का खण्डशः समाकलन (integration by parts) करने पर,

उपरोक्त समीकरण का प्रथम पद शून्य के बराबर होता है।

m तथा n को परस्पर प्रतिस्थापन करने पर.

समीकरण (4) से समीकरण ( 5 ) घटाने पर,

दूसरे समीकरण को सिद्ध करने के लिये लेजेंड्रे बहुपद के उदभ फलन का उपयोग करते हैं।

समीकरण (7) का वर्ग करने पर,

इसे – 1 से 1 के बीच x के सापेक्ष समाकलन करने पर,

समीकरण ( 6 ) से,

इन मानों को समीकरण (8) के समाकल में रखने पर,

इस समीकरण के दोनों तरफ z2n के गुणांकों की तुलना करने पर,

समीकरण (6) व (9) को एक समीकरण में संयुक्त करने पर,

जहाँ  क्रोनेकर डेल्टा फलन है। जब m = n,

P (x) के पुनरावृत्ति सम्बन्ध ( RECURRENCE RELATIONS OF Pn (x)) :  विभिन्न कोटि के बहुपद तथा उनके अवकलजों के बीच सम्बन्धों को पुनरावृत्ति सम्बन्ध (recurrence relation) कहते हैं। लेजेंड्रे बहुपद से सम्बन्धित छः पुनरावृत्ति सम्बन्ध होते हैं।

सम्बन्ध 1: (2n + 1) x Pn (x) = (n+1) Pn+1 (x) + nPn-1(x)

हम जानते हैं कि लेजेंड्रे बहुपद का उदभव फलन है,

समीकरण (1) का z के सापेक्ष अवकलन करने पर,

समीकरण के दोनों तरफ ( 1 – 2xZ + Z2 ) से गुणा करने पर,

 इस समीकरण के दोनों तरफ Zn के गुणांकों की तुलना करने पर,

सम्बन्ध 2 : nPn (x) = xP’n (x) – P’n-1(x)

समीकरण (1) का x के सापेक्ष अवकलन करने पर,

समीकरण (1) का z के सापेक्ष अवकलन करने पर,

समीकरण (4) को समीकरण (3) से भाग देने पर,

इस समीकरण के दोनों तरफ 2″ के गुणांकों की तुलना करने पर,

सम्बन्ध (1) का x के सापेक्ष अवकलन करने पर,

सम्बन्ध (2) से,

xP’n(x)= nPn(x) + P’n-1(x)

इस समीकरण को (2n + 1) से गुणा करने पर,

समीकरण ( 6 ) से समीकरण (7) घटाने पर,

सम्बन्ध 4. (n + 1) Pn(x) = P’n+1(x) = xP’n(x)

सम्बन्ध (3) से सम्बन्ध ( 2 ) घटाने पर,

सम्बन्ध ( 2 ) को x से गुणा करने पर,

(n+1) को n से प्रतिस्थापित करने पर,

समीकरण (11) से समीकरण (10) घटाने पर.

सम्बन्ध 6 : (1 – x2)P’n(x) = (n + 1) [xPn(x) – Pn+1(x)]

सम्बन्ध (1) से

यह समीकरण सम्बन्ध (5) में रखने पर,

(1 − x2)P’n(x) = (n + 1)[xPn(x) – Pn+1(x)] ………………………………(13)

सम्बन्ध 7 : क्रिस्टोफल विस्तारण (Christoffcl expansion)

सम्बन्ध (3) से,

इस समीकरण में n को (n-1) से प्रतिस्थापित करने पर,

P’n(x)=(2n-1) Pn-1(x) + P’n-2(x)…………………….(14)

इस समीकरण में n को (n – 2) से प्रतिस्थापित करने पर,

P’n-2(x)=(2n-5)Pn-3(x) + P’n-4(x) …………………………(15)

समीकरण (14) में समीकरण (15) रखने पर,

इसी प्रकार समीकरण ( 14 ) में n को (n – 4 ) से प्रतिस्थापित करने पर,

समीकरण ( 16 ) में समीकरण ( 17 ) रखने पर,

यह प्रक्रिया तब तक जारी रखी जा सकती है जब तक श्रेणी के अंत में n सम पूर्णांक होने पर 3P1 (x) तथा n विषम पूर्णांक होने पर Po (x) न प्राप्त हो जाये। यह विस्तारण क्रिस्टोफल विस्तारण कहलाता है।

सह-लेजेंड्रे समीकरण ( ASSOCIATED LEGENDRE EQUATION) सह-लेजेंड्रे अवकल समीकरण लेबनिट्ज प्रमेय (Leibnitz theorem) की सहायता सेलेजेंड्रे अवकल समीकरण को m बार अवकलित करके प्राप्त किया जा सका है। लेबनिट्ज प्रमेय के कथन के अनुसार,

लेजेंड्रे अवकल समीकरण को लिखने पर,

इस प्रमेय का उपयोग करके लेजेंड्रे समीकरण को m बाद अवकलित करने पर,

इन अवकलजों को समीकरण (1) में रखने पर,

यह अवकल समीकरण सह लेजेंड्रे समीकरण कहलाता है। इस समीकरण में m = 0 रखने पर यह लेजेंड्रे समीकरण में परिवर्तित हो जाती है। चूँकि यह समीकरण w (x) द्वारा संतुष्ट होता है। इसलिये इस समीकरण का हल करेगा।

w(x) सह-लेजेंड्रे बहुपद कहलाता है तथा इसे PnM (x) द्वारा व्यक्त करते हैं।

सह-लेजेंड्रे बहुपद के कुछ उपयोगी परिण

(i) चूँकि लेजेंड्रे बहुपद Pn (x) में x का अधिकतम घात xn होता है इसलिये

 Pn(x) a munter frчUT (GRAPHICAL REPRESENTATION OF P(x))

रोड्रिग सूत्र से

n के विशिष्ट मानों के लिये लेजेंड्रे बहुपद ज्ञात किये जा सकते हैं।

कुछn (n = 0, 1, 2, 3, 4) के विशिष्ट मानों के लिये Pn(x) तथा x में ग्राफ के आलेख चित्र (7.10.1) में दर्शाये गये हैं।

ग्राफ में

Po(x) = 1, x- अक्ष के समांतर एकांक दूरी पर सरल रेखा है।

P1(x) = x, मूल बिन्दु से पारित X- अक्ष से 45° कोण बनाती हुई सरल रेखा है।

 y – अक्ष के सममित परवलय है जिसका शीर्ष (0, 2) है।

मूल बिन्दु से पारित वक्र है।

 बिन्दु (0, 3/8) से पारित y-अक्ष के सममित वक्र है।