माइकलसन मोर्ले प्रयोग क्या है , इंटरफेरोमीटर , माइकेल्सन व्यतिकरणमापी सिद्धांत नोट्स michelson morley experiment in hindi

michelson morley experiment in hindi माइकलसन मोर्ले प्रयोग क्या है , इंटरफेरोमीटर , माइकेल्सन व्यतिकरणमापी सिद्धांत नोट्स ?

माइकलसन मोरले प्रयोग (निरपेक्ष जड़त्वीय निर्देश तन्त्र की खोज) (Michelson-Morley Experiment)
न्यूटन के अनुसार दूरी, समय तथा द्रव्यमान भौतिक राशियाँ निरपेक्ष तथा नियत होती है और प्रेक्षक तथा प्रेक्षण स्थिति पर निर्भर नहीं करती हैं। इनके अतिरिक्त न्यूटन ने एक ऐसे नदश तन्त्र
पष्ट का जो इस ब्रह्माण्ड में स्थिर तथा निरपेक्ष हो जिसके सापेक्ष पिण्डों की निरपेक्ष गन को जाना जा सके तथा प्रायोगिक प्रेक्षित परिणामों को निरपेक्ष गति के पदों में ज्ञात किया जा सके। परन्तु न्यूटन ने अन्त में यह स्वीकार किया कि किसी निकाय में रहकर निकाय की निरपेक्ष गति का किसी भी यात्रिक उपकरण द्वारा पता नहीं लगाया जा सकता है। दसरे शब्दों में हम यह कह सकते हैं कि अन्य पिण्डों के सापेक्ष पिण्ड का वेग ही सार्थक होता है. निरपेक्ष वेग का यथार्थ में कोई महत्व नहीं होता

प्रकाश क सचरण की प्रकृति की व्याख्या करने के लिए दिये गये एक विशेष परिकल्पना ने निरपेक्ष दश फ्रम तथा निरपेक्ष गति की समस्या को प्रकाशीय उपकरणों द्वारा हल करने के लिए पुनः आशान्वित किया। इस परिकल्पना के अनुसार प्रकाश तरंगें एक काल्पनिक प्रकाशवाही ईथर (luminiferous ether) माध्यम म गति करती हैं | यह ईथर सर्वव्यापी अर्थात सम्पूर्ण ब्रह्माण्ड तथा पदार्थों के अन्दर विद्यमान होता है। विभिन्न वैज्ञानिकों ने ईथर की परिकल्पना को निरपेक्ष निर्देश तन्त्र की खोज के लिए उपयोग किया और इस पर विचार किया कि ईथर का क्या होता है ? इस सम्बन्ध में विभिन्न वैज्ञानिकों ने भिन्न-भिन्न विचार प्रकट किये। इनमें से दो निम्न प्रमुख विचार हैं1. गतिशील पिण्ड अपने साथ ईथर को घसीटते हैं। फलतः पिण्ड तथा ईथर के मध्य सापेक्ष गति नहीं होगी और गतिशील पिण्ड के सापेक्ष प्रकाश के वेग में कोई परिवर्तन नहीं होगा। अतः किसी प्रकाशीय घटना द्वारा पिण्ड की निरपेक्ष गति को ज्ञात नहीं किया जा सकता है।
2. यदि पिण्ड स्थिर ईथर माध्यम में गति करते हैं अर्थात् गतिमान पिण्ड अपने साथ ईथर को नहीं घसीटती है तो इसके परिणामस्वरूप निरपेक्ष ईथर तथा पिण्ड के मध्य सापेक्ष गति होगी और पिण्ड की सापेक्ष गति प्रकाश के वेग में परिवर्तन कर देगा, जिसे प्रकाशीय घटना द्वारा संसूचित (detect) किया जा सकता है।
अत: निरपेक्ष ईथर तथा पृथ्वी (पिण्ड) के मध्य सापेक्ष गति के कारण प्रकाश के वेग में परिवर्तन को ज्ञात करने के लिए कई प्रयोग किये गये। उनमें से सबसे महत्वपूर्ण प्रयोग माइकलसन-मोरले का प्रयोग है जो प्रकाश के व्यतिकरण सिद्धान्त पर आधारित है।

 माइकलसन-मोरले प्रयोग का सिद्धान्त

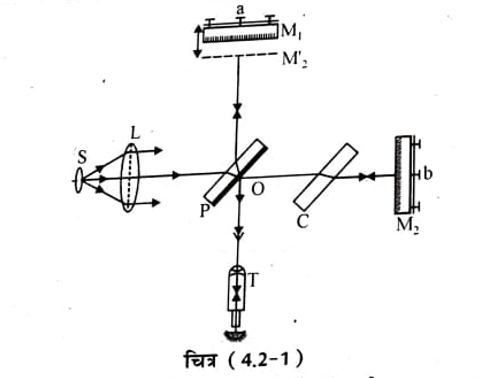
– यदि स्थिर ईथर तथा पृथ्वी के मध्य सापेक्ष गति के कारण प्रकाश के वेग में परिवर्तन संभव मान लें तो एक स्थिति में प्रकाश किरण पुंज पृथ्वी की गति की दिशा में निश्चित दूरी तक गति कर लौट आये तथा दूसरी स्थिति में प्रकाश किरण पुंज पृथ्वी की गति की दिशा के लम्बवत् समान दूरी तय कर लौट आये तो दोनों स्थितियों में प्रकाश किरण पुंज द्वारा व्यतीत किये गये समयों में अन्तर होगा इस समयान्तर की प्रयोगिक तरीकों से जैसे, माइकलसन-व्यतिकरणमापी (Michelson interferometer) द्वारा नापा जा सकता है | चित्र में इस कल्पना को दर्शाया गया है और अन्य चित्र में माइकलसन मोरले द्वारा उपयोग में लाये गए व्यतिकरणमापी को प्रदर्शित किया गया है |

चित्र (2) के अनुसार जब एक वर्णी प्रकाश स्रोत S से निर्गत प्रकाश किरण पुंज 45° पर झुके अर्ध रजतित (half silvered) प्लेट P पर आपतित होती है तो वह समान आयाम की परस्पर लम्बवत् परावर्तित (Oa दिशा में) एवं पारगमित (Ob दिशा में) दो किरण पुंजों में विभाजित हो जाती हैं। ये दोनों किरणें उनकी दिशाओं में प्लेट P से समान दूरी पर स्थित क्रमशः दर्पण M1 तथा M2 पर अभिलम्बवत् आपतित होती हैं तथा परावर्तित होकर लोटती हैं। aO तथा bO दिशा में परावर्तित किरणें विभाजक प्लेट P पर पुनः लौट आती है तथा प्लेट P से पारगमित व परावर्तित होकर अध्यारोपण से व्यतिकरण की फ्रिन्जें बनती हैं जिन्हें दूरदर्शी (telescope) T की सहायता से देखा जाता है। ये व्यतिकरण फ्रिज्में सकेन्द्रिक वृतों के रूप में दिखाई पड़ती हैं।

प्लेट P के समान मोटाई की एक अन्य प्लेट C इसके समान्तर Ob पथ में रखते हैं ताकि OM1 तथा OM2 की वास्तविक दूरी बराबर होने के साथ-साथ उनकी प्रकाशीय दूरी भी बराबर हो जायें। सम्पूर्ण उपकरण पारे के एक कुण्ड (tank) में तैरता रहता है ताकि इसे ऊर्ध्वाधर अक्ष पर आवश्यकता अनुसार घुमाया जा सके।

यदि Oa तथा Ob प्रकाश किरणों का प्रकाशीय पथ बराबर है और ईथर के सापेक्ष उपकरण स्थिर है तो दोनों किरणें 0 बिन्दु पर लौटने में समान समय लेंगी अर्थात् दोनों किरणें एक ही कला में पहुंचेगी। अब हम कल्पना करते हैं कि सम्पूर्ण उपकरण ईथर के सापेक्ष पृथ्वी के वेग v से Ob दिशा में गति कर रहा है तो Ob दिशा में जाते समय प्रकाश का वेग (c-v) तथा bo दिशा में लौटते समय प्रकाश का वेग (c + v) होगा, चित्र (3)। यदि Ob पथ की लम्बाई d है तो प्रकाश द्वारा 0 से b तक जाने तथा b से 0 तक लौटने में लिया गया कुल समय

t₁ = d/c-v  + d/c+v

= 2dc/(c²-v²)

= 2d/c (1-v²/c²)^-1

या

t₁ = 2d/c (1+v²/c²)

[द्विपद प्रमेय का उपयोग करने और v²/c² के उच्च घात वाले पदों को उपेक्षणीय मानने पर , क्योंकि v<<c]

अब हम Oa दिशा में परिवर्तित किरण के बारे में विचार करते है जो ईथर के सापेक्ष वेग v से गतिशील उपकरण के लम्बवत दिशा में गति करती है | O से M₂ दर्पण की दूरी भी d रखते है | प्लेट P से परावर्तन के पश्चात् M₁ दर्पण की तरफ जाने वाली प्रकाश किरण जब तक दर्पण M₁ पर पहुंचेगी तब तक दर्पण M₁ अपनी नयी स्थिति M₂ तक पहुँच जाएगी | यदि किरण Oa’ दूरी तय करने में समय t₂₁ लेती है तो इतने समय में दर्पण M₁ दूरी aa’ = vt₂₁ तय कर लेगा |