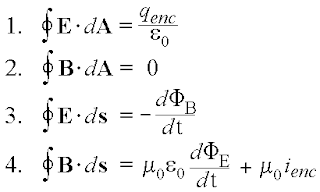मैक्सवेल की समीकरण : मैक्सवेल के समीकरण कौन कौन से है (Maxwell’s equations in hindi)

SbistudyDecember 15, 2018inPhysics

मैक्सवेल की समीकरण : मैक्सवेल के समीकरण कौन कौन से है (Maxwell’s equations in hindi) जेम्स क्लार्क मैक्सवेल की विद्युत चुम्बकीय तरंगों से सम्बन्धित सभी समीकरणों को लिखिए | समीकरणे क्या है ? maxwell electromagnetic equation |

प्रस्तावना : विद्युत चुम्बकीय की दुनिया को पूर्ण रूप से समझने के लिए अर्थात विद्युत चुंबकीय को पूर्ण रूप से समझाने के लिए मैक्सवेल ने अपनी चार समीकरण दी।
ये चारों समीकरण इस बात पर आधारित है कि किसी विद्युत चुम्बकीय तरंग में विद्युत क्षेत्र , चुम्बकीय क्षेत्र कैसे संचरित होते है तथा आपस में कैसे सम्बन्ध रखते है तथा साथ ही जब ये किसी वस्तु पर टकराती है या गुजरती है तो वस्तु के साथ इसका व्यवहार कैसा रहता है ऐसी बातों की जानकारी देती है क्यूंकि समीकरण देने से पहले मैक्सवेल ने इन सभी बातों पर बहुत अध्ययन करने के बाद विद्युत चुम्बकीय तरंगों के लिए अपने ये चार समीकरण दिए।
जेम्स कलर्क मैक्सवेल (1831-1879) ने पहले से दिए हुए समीकरणों और नियमों की सहायता ली जैसे फैराडे का नियम और एम्पीयर का नियम आदि और इनकी सहायता से और इन ज्ञात समीकरणों का उपयोग करते हुए अपने चार समीकरण दिए जिन्हें मैक्सवेल के समीकरण कहते है और इन चार समीकरणों की सहायता से विद्युत चुम्बकीय तरंगों की पूरी व्याख्या की जा सकती है।
मैक्सवेल ही पहले वो वैज्ञानिक थे जिन्होंने विद्युत चुम्बकीय तरंगों के वेग की गणना की थी और बताया था कि विद्युत चुंबकीय तरंगें प्रकाश के वेग से गति करती है या संचरित होती है।
मैक्सवेल ने विद्युत चुम्बकत्व और स्थिर चुम्बकत्व आदि के नियमों को मिलाया और इनकी सूत्रों की सहायता से मैक्सवेल ने विद्युत चुम्बकीय सिद्धांत के अपने चार नियमों का एक सेट दिया जिन्हें मैक्सवेल के समीकरण कहते है।
मैक्सवेल ने अपने सभी नियम विभिन्न प्रयोग करने के बाद उनके निष्कर्ष के आधार पर दिए और सभी समीकरणों का उपयोग करके विद्युत चुम्बकीय की सभी घटनाओं की अच्छी तरह से व्याख्या करने में सक्षम है।
मैक्सवेल द्वारा दिए गए चार समीकरण निम्न है –

ऊपर चार समीकरण प्रदर्शित है जिनकी व्याख्या निम्न है –
समीकरण 1 को गॉस का नियम कहते है जिसके अनुसार किसी भी बंद पृष्ठ से गुजरने वाला विद्युत फ्लक्स , पृष्ठ द्वारा परिबद्ध नेट आवेश q तथा विद्युतशीलता नियतांक के भागफल के बराबर होता है।
समीकरण 2 को चुम्बकत्व में गॉस का नियम कहलाता है , इसके अनुसार किसी बंद पृष्ठ से गुजरने वाला नेट चुम्बकीय फ्लक्स का मान शून्य होता है।
समीकरण 3 को विद्युत चुम्बकीय प्रेरण का फैराडे का नियम कहा जाता है , इस नियम या समीकरण के अनुसार एक परिवर्तित चुम्बकीय क्षेत्र द्वारा विद्युत क्षेत्र उत्पन्न होता है।
समीकरण 4 को मैक्सवेल का नियम कहते है जिसे मैक्सवेल ने अम्पीयर के नियम को संशोधित करने के बाद प्राप्त किया , इस नियम के अनुसार केवल चालन धारा ही चुम्बकीय क्षेत्र उत्पन्न नहीं करती है , परिवर्तित विद्युत फ्लक्स भी चुम्बकीय क्षेत्र उत्पन्न करता है।
इस प्रकार मैक्सवेल न अपने चार समीकरण दिए और इन्हें हम यहाँ विस्तार से पढ़ चुके है।

मैक्सवेल के समीकरण (maxwell’s equations) : वैज्ञानिक जेम्स क्लार्क मैक्सवेल ने विद्युत और चुम्बकत्व के नियमों को जिन अवकल समीकरणों द्वारा गणितीय रूप प्रदान किया उन्हें मैक्सवेल के समीकरण कहते है। मैक्सवेल के निम्नलिखित चार समीकरण है –

1. स्थिर वैद्युत का गॉस नियम : इस नियम के अनुसार किसी स्वेच्छग्रहित बंद पृष्ठ से सम्बद्ध वैद्युत फ्लक्स पृष्ठ द्वारा परिबद्ध आवेश का 1/ε₀ गुना होता है अर्थात

∮E.ds = q/ε₀

यहाँ ds क्षेत्रफल अल्पांश है तथा q गाउसीय पृष्ठ द्वारा परिबद्ध आवेश है।

2. स्थिर चुम्बकत्व का गॉस नियम : इस नियम के अनुसार किसी बंद पृष्ठ से सम्बद्ध चुम्बकीय फ्लक्स सदैव शून्य होता है अर्थात

∮B.ds = 0

नोट : यह नियम यह प्रदर्शित करता है कि प्रकृति में विलगित चुम्बकीय ध्रुव का अस्तित्व नहीं है।

3. फैराडे का विद्युत चुम्बकीय प्रेरण का नियम : इस नियम के अनुसार किसी बंद परिपथ में प्रेरित विद्युत वाहक बल परिपथ से बद्ध चुम्बकीय फ्लक्स में परिवर्तन की ऋणात्मक दर के बराबर होता है अर्थात प्रेरित विद्युत वाहक बल

e = -dɸ_m/dt

यदि पृष्ठ की सीमा रेखा पर लम्बाई के खण्ड dl की स्थिति पर विद्युत क्षेत्र E हो तो विद्युत वाहक बल

_c∫ E.dl = -dɸ_m/dt

4. एम्पियर का संशोधित नियम : इस नियम के अनुसार किसी बंद पथ की सीमा के अनुदिश चुम्बकीय क्षेत्र का रेखीय समाकलन चालन धारा और विस्थापन धारा के योग का μ₀ गुना होता है अर्थात

∮B.dl = μ₀(I_c + I_D) = μ₀(I_c + ε₀ ϑΦ_E/ϑt)

स्पष्ट है कि परिवर्ती विद्युत क्षेत्र चुम्बकीय क्षेत्र उत्पन्न करता है।