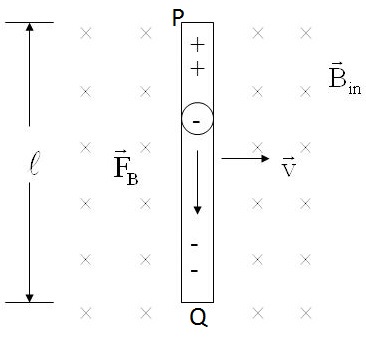
Induced emf in a conductor rod moving in a uniform magnetic field in hindi समरूप चुम्बकीय क्षेत्र में चालक छड की गति के कारण प्रेरित वि.वा.बल  : माना कागज के लम्बवत निचे की तरफ एक चुम्बकीय क्षेत्र B उपस्थित है , यह समरूप से फैला हुआ है।

इस चुम्बकीय क्षेत्र में एक l लम्बाई का चालक रखा हुआ है इसे PQ से चित्र में दर्शाया गया है , यह कागज तल में रखा हुआ है अत: यह चुम्बकीय क्षेत्र के लम्बवत स्थित है , क्यूंकि चुम्बकीय क्षेत्र कागज तल के लम्बवत निचे की तरफ उपस्थित है।
अब यदि इस चालक को कागज तल में V वेग से गति कराये तो इसका अभिप्राय यह होगा की यह चालक चुम्बकीय क्षेत्र के लम्बवत गति कर रहा है अत: लोरेन्ज के अनुसार इसके आवेशो पर लोरेंज बल लगेगा।
चूँकि हम जानते है की किसी चालक में मुक्त इलेक्ट्रॉन होते है अतः चालक की गति के साथ इसमें उपस्थित मुक्त इलेक्ट्रॉन भी गति करेंगे अत: इन गतिशील इलेक्ट्रॉनो पर चुम्बकीय बल कार्य करेगा जिसका मान निम्न सूत्र द्वारा दिया जाता है
Fmagnetic = qVBsinθ
चूँकि यहाँ आवेश की गति V तथा चुंबकीय क्षेत्र B एक दूसरे के लंबवत है अर्थात इनके मध्य 90 डिग्री का कोण है
अत: θ = 90
Fmagnetic = qVBsin90
Fmagnetic = qVB
यहाँ q इलेक्ट्रॉन पर आवेश है।
इस चुम्बकीय बल की दिशा ज्ञात करने के लिए फ्लेमिंग का बायें हाथ का नियम काम में लिया जाता है , इस नियम के अनुसार यह लोरेन्ज बल धनावेश पर चालक के P सिरे की ओर कार्य करता है तथा ऋणावेश पर Q सिरे की ओर कार्य करता है।
दूसरे शब्दों में कहे तो इस बल के कारण P सिरे पर धनावेश तथा Q सिरे पर ऋणावेश इकठ्ठा हो जाता है जिससे P सिरा धनावेशित हो जाता है तथा Q सिरा ऋणावेशित हो जाता है जैसा चित्र में दिखाया गया है।
सिरों पर उत्पन्न इन विपरीत प्रकृति के आवेशों के कारण दोनों सिरों के मध्य एक विभवान्तर(e) उत्पन्न हो जाता है तथा इस विभवांतर(e) के कारण चालक में एक विद्युत क्षेत्र उत्पन्न हो जाता है , इस विद्युत क्षेत्र (E) की दिशा P से Q की तरफ होगी।
अतः चुम्बकीय बल के विपरीत दिशा में विद्युत क्षेत्र के कारण आवेशों पर विद्युत बल कार्य करेगा जिसका मान निम्न सूत्र द्वारा लिखा जाता है
FElectric = qE
यहाँ q = आवेश तथा E = विद्युत क्षेत्र
चूँकि चुम्बकीय बल तथा विद्युत बल एक दूसरे के विपरीत दिशा में कार्यरत है अतः संतुलन की स्थिति में दोनों बल एक दूसरे के बराबर होते है
अर्थात
Fmagnetic = FElectric 
qVB = qE 
VB = E 
यहाँ
विद्युत क्षेत्र = उत्पन्न वि.वा.बल /चालक की लम्बाई
E = e /l
E का मान समीकरण में रखने पर
E = VB
e /l = VB
e = VBl
मान लीजिये चालक की गति चुम्बकीय क्षेत्र के लंबवत न होकर किसी कोण θ पर हो तो
e = VBl sinθ
संतुलन की स्थिति में परिणामी बल शून्य हो जाता है अर्थात दोनों बिन्दुओ PQ के मध्य विभवांतर शून्य हो जाता है जिससे आवेश का स्थानान्तरण भी नहीं होता है।

सब्सक्राइब करे youtube चैनल

हिंदी माध्यम नोट्स

Class 6

Hindi social science science maths English

Class 7

Hindi social science science maths English

Class 8

Hindi social science science maths English

Class 9

Hindi social science science Maths English

Class 10

Hindi Social science science Maths English

Class 11

Hindi sociology physics physical education maths english economics geography History

chemistry business studies biology accountancy political science

Class 12

Hindi physics physical education maths english economics

chemistry business studies biology accountancy Political science History sociology

Home science Geography

English medium Notes

Class 6

Hindi social science science maths English

Class 7

Hindi social science science maths English

Class 8

Hindi social science science maths English

Class 9

Hindi social science science Maths English

Class 10

Hindi Social science science Maths English

Class 11

Hindi physics physical education maths entrepreneurship english economics

chemistry business studies biology accountancy

Class 12

Hindi physics physical education maths entrepreneurship english economics

chemistry business studies biology accountancy