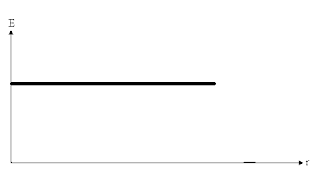हिंदी में गाऊसी सतह , gaussian surface in hindi , गॉसीय पृष्ठीय आवेश , रेखीय , बिंदु , गाउसीय पृष्ठ :-
गॉसीय पृष्ठ : एक ऐसा काल्पनिक पृष्ठ जिसके प्रत्येक बिंदु पर विद्युत क्षेत्र की तीव्रता समान हो , गाउसीय पृष्ठ कहलाता है।
गाउसीय पृष्ठ को बंद आकृति में परिवर्तित करने के लिए ऐसे पृष्ठों का चयन करते है जिनका तल या तो विद्युत क्षेत्र के समान्तर हो या विद्युत क्षेत्र के लम्बवत हो।
गाउसीय पृष्ठ (gaussian surface in hindi) : कूलाम के नियम के द्वारा केवल सरल परिस्थतियों में विद्युत क्षेत्र की तीव्रता का व्यंजक प्राप्त किया जा सकता है। उन परिस्थितियों में जहाँ कुलाम के नियम एवं अध्यारोपण के सिद्धांत के द्वारा विद्युत क्षेत्र की गणना नहीं कर सकते , वहां इन्हें गॉस के प्रमेय की सहायता से प्राप्त कर सकते है। इसके लिए सबसे पहले पृष्ठ समाकलन की गणना करनी पड़ती है। आवेश वितरण के चारों ओर चतुराई से एक ऐसा बंद पृष्ठ चुनना पड़ता है , जिससे पृष्ठ समाकलन को आसानी से प्राप्त किया जा सके , जिस पृष्ठ को चुना जाता है , वही गाउसीय पृष्ठ कहलाता है।
गाउस के अनुप्रयोग
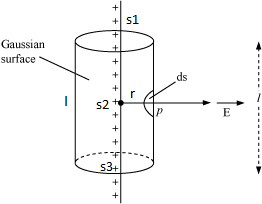
1. अनन्त लम्बाई के रेखीय आवेश के कारण विद्युत क्षेत्र की तीव्रता : माना एक अनंत लम्बाई का रेखाएँ आवेश जिसका रेखीय आवेश घनत्व λ है। इस रेखीय आवेश से लम्बवत r दूरी पर स्थित बिन्दु P पर विद्युत क्षेत्र की दिशा ज्ञात करने के लिए –
अन्नत लम्बाई के रेखीय आवेश पर स्थित बिंदु O से लम्बवत दूरी r पर स्थित बिंदु p पर विद्युत क्षेत्र की दिशा ज्ञात करने के लिए बिंदु O से समान दूरी पर दो अल्पांश dl1 व dl2 ऊपर व नीचे लेते है . इन अल्पांशो के कारण बिंदु p पर प्राप्त विद्युत क्षेत्र की तीव्रताए क्रमशः dE1 व dE2 को घटकों में वियोजित करने पर घटक dE1sinθ व dE2sinθ परिमाण में समान व दिशा में एक दूसरे के विपरीत होने के कारण एक-दुसरे के प्रभाव को निरस्त कर देते है तथा घटक dE1cosθ व dE2cosθ परिमाण में समान व एक ही दिशा में होने के कारण इन घटकों के अनुदिश विद्युत क्षेत्र की दिशा प्राप्त होती है अर्थात रेखीय आवेश के लम्बवत बाहर या अन्दर की ओर विद्युत क्षेत्र की दिशा प्राप्त होती है।
माना रेखीय आवेश का रेखीय आवेश घनत्व ‘λ’ है इस रेखीय आवेश से लम्बवत ‘r’ दूरी पर स्थित बिंदु p पर विद्युत क्षेत्र की तीव्रता की गणना के लिए ‘r’ त्रिज्या के बेलनाकार गाउसीय पृष्ठ की कल्पना करते है।
यदि बेलनाकार गाउसीय पृष्ठ की लम्बाई L हो तो बेलनाकार पृष्ठ से परिबद्ध कुल आवेश Σq = λ.L
गाउस के नियम से –
∫E.dS = Σq/E0
∫s1 E.dS + ∫s2 E.dS + ∫s3 E.dS = Σq/E0
∫s1 E.dS.cos90 + ∫s2 E.dS.cos0 + ∫s3 E.dS.cos90 = Σq/E0
0 + ∫s2 E.dS + 0 = Σq/E0
∫s2 E.dS = Σq/E0
Σq का मान रखने पर –
∫s2 E.dS = λ.L/E0
यहाँ बेलनाकार गाउसीय पृष्ठ का क्षेत्रफल ∫s2 dS = 2π.r.L
अत:
E.(2π.r.L) = λ.L/E0
E = λ/2π.r.E0
ऊपर और नीचे 2 से गुणा करने पर –
E = 2λ/4π.r.E0
चूँकि 1/4πE0 = K
अत:
E = 2kλ/r
अन्नत लम्बाई के रेखीय आवेश के कारण विद्युत क्षेत्र की तीव्रता व दूरी के मध्य ग्राफ निम्न प्रकार है –
2. अपरिमित अचालक परत के कारण विद्युत क्षेत्र की तीव्रता : माना कोई अपरिमित अचालक परत जिसका पृष्ठीय आवेश घनत्व सिग्मा (σ) है। इस अपरिमित अचालक परत से r दूरी पर स्थित बिंदु P पर विद्युत क्षेत्र की दिशा ज्ञात करने के लिए –
अपरिमित अचालक परत पर स्थित बिन्दु O से इसके लम्बवत ‘r’ दूरी पर स्थित बिंदु p पर विद्युत क्षेत्र की दिशा ज्ञात करने के लिए बिंदु O से समान दूरी पर ऊपर व नीचे दो पृष्ठीय अल्पांश ds1 व ds2 लेते है। dS1 व dS2 अल्पांशो के कारण बिंदु P पर प्राप्त विद्युत क्षेत्र की तीव्रताए क्रमशः dE1 व dE2 को घटकों में वियोजित करने घटक dE1sinθ व dE2sinθ परिमाण में समान (dS1 = dS2) व दिशा में एक दुसरे के विपरीत होने के कारण एक दूसरे के प्रभाव को निरस्त कर देते है परन्तु घटक dE1cosθ व dE2cosθ परिमाण में समान व एक ही दिशा मे होने के कारण इन घटकों के अनुदिश विद्युत क्षेत्र की तीव्रता की दिशा प्राप्त होती है अर्थात अचालक परत के लम्बवत अन्दर या बाहर विद्युत क्षेत्र की दिशा होती है।
माना अपरिमित अचालक पृष्ठ का पृष्ठीय आवेश घनत्व (σ) है। इस पृष्ठ से इसके लम्बवत ‘r’ दूरी पर स्थित बिंदु P पर विद्युत क्षेत्र की तीव्रता की गणना के लिए बेलनाकार गाउसीय पृष्ठ की कल्पना करते है।
जब प्रत्येक वृत्ताकार गाउसीय पृष्ठ क्षेत्रफल S हो तो इस बेलनाकार पृष्ठ से परिबद्ध कुल आवेश (Σq = σS ) ……. [समीकरण-1] (पृष्ठीय आवेश घनत्व की परिभाषा से)
गाउस के नियम से –
∫E.dS = Σq/E0
∫s1 E.dS + ∫s2 E.dS + ∫s3 E.dS = Σq/E0
∫s1 E.dS.cos 0 + ∫s2 E.dS.cos90 + ∫s3 E.dS.cos0 = Σq/E0
∫s1 E.dS + 0 + ∫s3 E.dS = Σq/E0
[समीकरण-1] से Σq का मान रखने पर –
किसी अपरिमित चालक परत या चालक पृष्ठ या चालक सतह के कारण विद्युत क्षेत्र की तीव्रता का मान वही होता है जो अपरिमित अचालक परत के कारण होता है।