ELECTRIC POTENTIAL INSIDE RECTANGULAR CONDUCTING BOX in hindi आयताकार चालक बॉक्स के अन्दर विद्युत विभव

आयताकार चालक बॉक्स के अन्दर विद्युत विभव कितना होता है

आयताकार चालक बाक्स के अन्दर विद्युत विभव (ELECTRIC POTENTIAL INSIDE RECTANGULAR CONDUCTING BOX) 

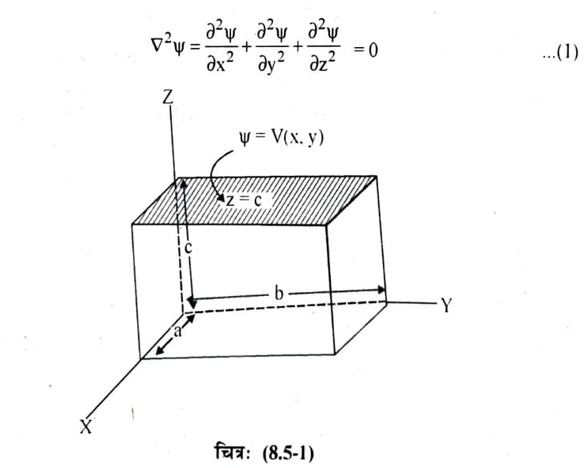
माना एक आयताकार चालक बाक्स की कल्पना करते है जिसकी भुजाएँ a,b ,c, कार्तीय निर्देश तंत्र की क्रमश: X, Y, Z अक्षों के अनुदिश है जैसा की चित्र ( 8.5 – 1) में दर्शाया गया है। फलक z = c के अतिरिक्त अन्य सभी फलकों x = y = z = 0, x = a एवं y = b पर विभव का मान शून्य है फलक z=c पर विभव का मान (x, y, z) = V(x, y) है। हम चालक बाक्स के अंदर विद्युत विभव ज्ञात करना चाहते हैं। इस स्थिति में त्रिविमीय निर्देशांक वाला लॉप्लास समीकरण का उपयोग करेंगे। 

इस समीकरण का हल (x, y, z) को तीन पृथक एकल चर वाले फलनों X(x), Y(y) व Z(z) के गुणनफल के रूप में व्यक्त कर सकते हैं-

जहाँ पिछले खण्ड के समीकरण ( 5 ) से,

(i) x = 0 पर विभव ৠ(x, y, z) = 0 अर्थात X(x) Y(y)Z(z) = 0, चूंकि Y(y) व Z(z), x के फलन नहीं है इसलिये X(x) = 0. इस प्रतिबंध को समीकरण (3a) में आरोपित करने पर,

0 = B cos BX

(ii) y = 0पर, विभव (x, y, z) = 0 अर्थात X(x)Y(y)Z(z) = 0. चूंकि X(x) इसलिये Z(2) = 0. इस प्रतिबंध को समीकरण (3c) में आरोपित करने  पर

0 = D cos Bx

(iii) इसी प्रकार z = 0 विभव (x, y, z) = 0 अर्थात X(x) Y(y) Z(z) = 0. Y(y) = 0, इस प्रतिबंध को समीकरण (3b) में

व Y(y), z के फलन नहीं है पर, 0 = B cos cx, 0 = D cos Bx, अत: B = 0. चूँकि X (x) व Z(z), y आरोपित करने पर, 

इन नियतांकों के मान समीकरण (3) में रखने पर लॉप्लास समीकरण का हल होगा।

 चूंकि समीकरण (1) का हल nam के सभी मानों के लिये वैध है इसलिये इसका व्यापक हल होगा-

(v) गुणांक Amn का मान ज्ञात करने के लिए समीकरण (5) में परिसीमा प्रतिबंध z = c पर U(x, y, z) = V(x, y) लगाते हैं-

इस समीकरण को दोनों तरफ गुणा करके अंतराल 0 < x

a < a व 0 < y < b के बीच x व y के सापेक्ष समाकलन करने पर,

परंतु हम जानते हैं कि

इसी प्रकार

इन समाकलनों को समीकरण (7) में रखने पर,

गुणांक Amn के मान को समीकरण (5), आयताकार बाक्स के अंदर किसी भी बिंदु (x, y) पर विभव मान ज्ञात किया जा सकता है।

गोलीय निर्देशांकों में लॉप्लास समीकरण (LAPLACE EQUATION IN SPHERICAL COORDINATES) 

लॉप्लास समीकरण  को गोलीय निर्देशांको  में निम्न रूप में लिखा जा सकता है-

चरों के पृथक्करण तकनीक का उपयोग कर अज्ञात फलन को एकल चर फलनों  के गुणनफल के रूप में लिखा जा सकता है-

समीकरण (2) को समीकरण (1) में रखकर फिर  से भाग देने पर

इस समीकरण का प्रथम पद केवल एक चर का फलन है इसलिए यह किसी नियतांक के बराबर होना चाहिए। सुविधा के लिए इस नियतांक को n (n+1) लेते हैं। अत:

समीकरण (3a) के हल के लिये, इसका निम्न हल मानते है –

R = Ara

यह हल समीकरण (3a) को अवश्य संतुष्ट करना चाहिये, इसलिये इसे समीकरण (3a) में रखने चूंकि

यह एक द्विघातीय समीकरण है। अतः इसके दो हल होंगे।

अतः समीकरण (3a) का सामान्य हल होगा

यदि हम समीकरण 3(b) को देंखे तो अंतिम पद चर राशि पर निर्भर नहीं करती है बल्कि केवल एक चर $ पर निर्भर करती है। अतः यह पद भी किसी अन्य नियतांक के बराबर होना चाहिए। माना यह पद नियतांक – m 2 के बराबर है। अत: समीकरण (3b) के अंतिम पद को लिख सकते है

यह सरल आवर्त दोलक का अवकल समीकरण है इसलिये इसका हल होगा

समीकरण (3b) के अंतिम पद को – m2 से प्रतिस्थापन करने से,

यह समीकरण गोलीय निर्देशांकों में सह- – लेजेंड्रे अवकल समीकरण होता है। अतः इसका हल होगा –

…………………..(8)

समीकरण (4), (6) व (8) को समीकरण ( 2 ) में रखने पर,

जहाँ A, B, C, D नियतांक है जिन्हें समस्या की परिसीमा प्रतिबंध से ज्ञात किया जा सकता है। चूंकि लॉप्लास समीकरण का हल m व n के सभी मानों के लिये वैध है इसलिये गोलीय निर्देशांकों में लॉप्लास समीकरण का व्यापक हल होगा –

 विद्युत क्षेत्र में स्थित भूसम्पर्कित चालक गोले के बाहर विभव (POTENTIAL OUTSIDE THE EARTHED CONDUCTING SPHERE PLACED IN AN ELECTRIC FIELD)

गोलीय निर्देशांकों में लॉप्लास समीकरण के उदाहरण के रूप में a त्रिज्या के चालक गोले के बाहर विभव का मान ज्ञात करना चाहते है जब इसका पृष्ठ भूसम्पर्कित है तथा यह 2- अक्ष अनुदिश एकसमान Eo तीव्रता वाले विद्युत क्षेत्र में स्थित है। चूंकि गोले का पृष्ठ भूसम्पर्कित है। इसलिए इस पर विभव का मान शून्य होगा अर्थात_y (a,0) = 0.

गोला चालक होने के कारण विद्युत विभव दिगंशी कोण (aximuthal angle) (p पर निर्भर नहीं करता है अर्थात m = 0. गोले के बाहर किसी बिंदु p पर विभव का मान लॉप्लास समीकरण V2 y = 0 द्वारा प्राप्त किया जा सकता है जिसका सामान्य हल पिछले खण्ड के समीकरण ( 9 ) से लिख सकते हैं।

जहाँ गोले के केंद्र के सापेक्ष बिंदु P के निर्देशांक (1, 0) हैं।

समीकरण (1) में परिसीमा प्रतिबंध r = a पर W (r, B) = 0 आरोपित करने पर,

यह मान समीकरण (1) में रखने पर,

गोले से अत्यधिक दूरी (r) विद्युत क्षेत्र Z – अक्ष के अनुदिश होता है इसलिये अत्यधिक दूरी पर विभव का मान होता है – 

समीकरण (2) में इस परिसीमा प्रतिबंध को आरोपित करने पर,

इस समीकरण के दोनो तरफ P) (x) से गुणा करके -1 व 1 के बीच x के सापेक्ष समाकलन करने पर,

बहुपद्ाम्बिका गुण से,

अतः एकसमान विद्युत क्षेत्र Eo में भूसम्पर्कित चालक गोले के बाहर अधिक दूरी पर विभव के दो भाग होते हैं, (i) विभव  जो आरोपित विद्युत क्षेत्र के कारण होता है तथा (ii) विभव जो द्विध्रुव आघूर्ण  वाले द्विध्रुव की भांति व्यवहार करने वाले गोले के कारण होता है। इसलिये द्विध्रुव के कारण विभव

यदि गोले के पृष्ठ पर आवेश घनत्व ० है तो गोले के पृष्ठ पर विद्युत क्षेत्र

अतः गोले के पृष्ठ पर प्रेरित आवेश घनत्व एकसमान नहीं होता है बल्कि 0 कोण पर निर्भर करता है।

नियत पृष्ठीय विभव वितरण वाले गोले के बाहर व अंदर विभव (POTENTIAL OUTSIDE AND INSIDE the Sphere HAVING FIXED SURFACE POTENTIAL DISTRIBUTION)

माना a त्रिज्या वाले मिले कंपृष्ठ पर विभव निम्न प्रकार से वितरित है

यह माना गया है कि गोले के बाहर व अंदर आवेश घनत्व शून्य है ताकि विभव वितरण को ज्ञात करने के लिये लॉप्लास समीकरण का उपयोग किया जा सके यह भी माना गया है कि अन्त पर विभव का मान शून्य हो जाता है। अतः इस समस्या के लिए परिसीमा प्रतिबंध को निम्न रूप से लिख सकते है –

(i) गोले के बाहर विभवः

गोले के बाहर किसी बिंदु P पर विभव का मान लॉप्लास समीकरण  द्वारा प्राप्त किया जा सकता है जिसका सामान्य हल खण्ड (8.5) के समीकरण ( 9 ) से लिख सकते है। इस समस्या में सममिति के कारण विभव दिगंशी कोण पर निर्भर नहीं करता है इसलिये m = () रखा जा सकता है। अतः

चूंकि अनंत पर विभव का मान शून्य होता है, इस प्रतिबंध को संतुष्ट करने के लिये यह आवश्यक है कि गुणांक A का मान शून्य हो । अतः समीकरण ( 1 ) में A = (0 का मान रखने पर, है

गोले के पृष्ठ पर

इस समीकरण में cos 6 = x रखने पर,

इस समीकरण के दोनों तरफ Pm(x) गुणा करके – 1 व 1 के बीच x के सापेक्ष समाकलन करने

लेजेंड़े बहुपद के लाम्बिकता गुण से,

समीकरण (2) में गुणांक B का मान रखने पर,

गोले के बाहर विभव

(ii) गोले के अंदर विभव r गोले के अंदर जब का मान शून्य की ओर अग्रसर होता है तो r (n+1) अनंत की ओर अग्रसर होता है जिसके कारण विभव का मान अनंत की ओर अग्रसर होता है परंतु गोले के अंदर विभव अनंत नहीं हो सकता है इसलिये r – (n+1) का गुणांक B अवश्य होना चाहिये। अतः गोले के अदंर

Bn = 0

अतः गोले के अदंर विभव

इस समीकरण में cos e = x रखने पर,

इस समीकरण के दोनो तरफ Pm (x) गुणा करके -1 व 1 के बीच x के सापेक्ष समाकलन करने

लेजेंड्रे बहुपद के उपरोक्त बताये गये लाम्बिकता गुण का उपयोग करने पर,

समीकरण (2) में गुणांक An का मान रखने पर,

गोले के अंदर विभव

यदि विभव वितरण फलन F(9) ज्ञात हो तो गोले के बाहर व अंदर समीकरण (3) व (5) से ज्ञात कर सकते है।