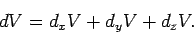विद्युत क्षेत्र एवं विद्युत विभव में सम्बन्ध electric field & electric potential relation in hindi
relation between electric field and electric potential in hindi विद्युत क्षेत्र एवं विद्युत विभव में सम्बन्ध : विद्युत क्षेत्र से विद्युत विभव के सूत्र स्थापन में हमने एक सम्बन्ध स्थापित किया था और इस संबंध के अनुसार दो बिंदुओं के मध्य विभवांतर तथा विद्युत क्षेत्र की तीव्रता निम्न प्रकार से सम्बन्धित है।
समविभव पृष्ठ के लिए विभव प्रवणता की दिशा पृष्ठ के लंबवत होती है।
माना चित्रानुसार दो समविभव पृष्ठ दिए गए है एक पृष्ठ के विभव का मान V तथा दूसरे पर विभव V-dV है।
चूँकि B तथा C बिंदु पर विभव का मान समान है अतः A बिन्दु से B व C के लिए विभव में कमी या हानि का मान समान dV होगा।
लेकिन AB व AC की दूरी भिन्न भिन्न है अतः विभव में दूरी के साथ परिवर्तन की दर भी अलग अलग dV/AB व dV/AC होगी।
क्योंकि दूरी AC का मान AB से अधिक है अर्थात AB < AC है अतः dV/AB > dV/AC
यहाँ विभव में हानि की दर पृष्ठ के अभिलम्ब दिशा में अधिकतम होगा।
यहां हम l को एक अक्ष मानकर समीकरण ज्ञात कर रहे है।
El = E COSθ , dl की दिशा में E
यदि अक्ष x , y , z अक्षो में है तो
चूँकि
अतः
अतः
E = ∇ V
यहाँ इसे ∇ को डेल संकारक (del operator) कहते है।
यदि यहां विभव को गोलीय पृष्ठ के लिए अर्थात त्रिज्या r के रूप में लिखने पर
Er = -dV/dr
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics