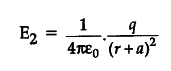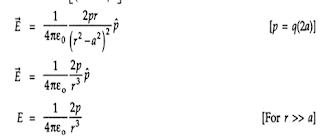विद्युत द्विध्रुव के कारण उसकी अक्षीय रेखा पर स्थित बिन्दु पर विद्युत क्षेत्र की तीव्रता electric field at point on the axial line
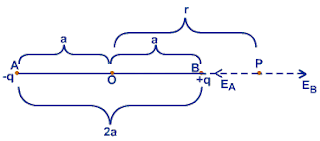
(electric field at point on the axial line of an electric dipole in hindi) विद्युत द्विध्रुव के कारण उसकी अक्षीय रेखा पर स्थित बिन्दु पर विद्युत क्षेत्र की तीव्रता :
p (विद्युत आघूर्ण) की दिशा ऋण आवेश से धन आवेश की ओर होती है अतः p (विद्युत आघूर्ण) व E (विद्युत क्षेत्र ) की एक ही दिशा दिशा होगी।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics