clapeyron equation thermodynamics in hindi क्लेपिरॉन समीकरण क्या है सूत्र क्लोसियस (Clausius)

क्लेपिरॉन समीकरण क्या है सूत्र क्लोसियस (Clausius) clapeyron equation thermodynamics in hindi

क्लेपिरॉन समीकरण (Clapeyron Equation)

क्लेपिरॉन समीकरण एक उपयोगी ऊष्मागतिक समीकरण है, जिसका उपयोग भौतिक साम्यवस्था के अध्ययन में किया जाता है। इस समीकरण को गिब्ज हैल्मोल्ट्स समीकरण द्वारा व्युत्पन्न किया जाता है । एक तन्त्र

द्रव = वाष्प का अध्ययन करते हैं ।

माना कि एक मोल द्रव को एक पिस्टन युक्त पात्र में लिया जाता है । द्रव का आयतन V1और वाष्प दाब p है। अब इस द्रव का स्थिर ताप T पर उत्क्रमणीय रूप से वाष्पीकरण होने देते हैं । जब सम्पूर्ण द्रव वाष्प में परिवर्तित हो जाता है तो कुल आयतन V2 हो जाता है।

वाष्पन में किया गया कार्य w = p(V2 – V1) ……………………….(1)

समीकरण (i) का अवकलन करने पर

(ii) वाष्पन में माना कि ऊष्मा L का अवशोषण होता है अतः L वाष्पन की गुप्त ऊष्मा (Latent heat of vaporisition) है। ऊष्मागतिकि के प्रथम नियम के अनुसार

E = w – L ……………………………..(iii)

समीकरण (ii) और (iii) के मान गिब्ज हैल्मोल्ट्स समीकरण में रखने पर

समीकरण (51) क्लेपीरॉन समीकरण कहलाती है।

समीकरण ( 51 ) को सामान्यरूप से भिन्न रूप से व्यक्त किया जाता है।

एक निश्चित ताप T पर किसी पदार्थ का एक निश्चित द्रव्यमान जिसका आयतन V1 है आयतन V2 में परिवर्तित होता है तो ऊष्मा परिवर्तन H है।

H को पदार्थ की संक्रमण ऊष्मा (Heat of transition) कहते हैं।

क्लोसियस – क्लेपीरॉन समीकरण (Clausius Clapeyron Equation) क्लेपीरॉन समीकरण में यदि द्रव के आयतन V1 को वाष्प के आयतन V2 की अपेक्षा नगण्य मान लिया जाये तो समीकरण ( 52 ) को सरल रूप से निम्न प्रकार लिखा जा सकता है-

यदि वाष्प आदर्श गैस के समान व्यवहार करती है तो एक मोल के लिये गैस समीकरण द्वारा

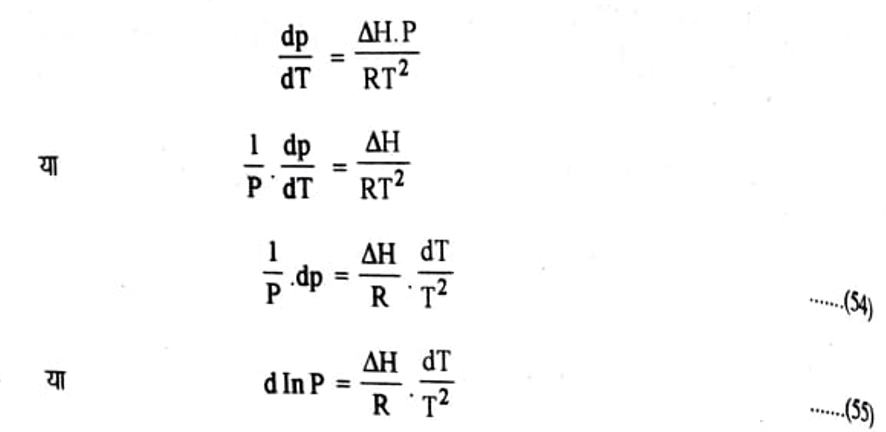
समीकरण (i) का मान समीकरण (53) में रखने पर

समीकरण (54) तथा (55) क्लॉसियस-क्लेपीरॉन समीकरण कहलाती है।

यदि H का मान स्थिर (Constant) मान लिया जाये तो समीकरण (55) का समाकलन करने पर

किसी द्रव का क्वथनांक यदि दाब P1पर ज्ञात हो तो उसका क्वथनांक दाब P2 पर ज्ञात किया जा सकता है।

क्लास्यिस क्लेपीरान समीकरण के उपयोग (Application of Clausius Clapeyron Equation) (i) वाष्पन की गुप्त ऊष्मा की गणना (Calculation of Latent Heat of Vaporisation):-

यदि दो ताप T1 तथा T2 पर किसी द्रव के वाष्पदाब P1 तथा P2 ज्ञात हों तो वाष्पन की गुप्त ऊष्मा(Hv ) की गणना की जा सकती है

(iii) अन्य ताप पर वाष्प दाब की गणना (Calculation of Vapour pressure at another Temperature):- यदि किसी द्रव का वाष्व दाब (P1) एक ताप (T1) पर ज्ञात हो तो उसका वाय दाब (P2) अन्य किसी ताप (T2) पर ज्ञात किया जा सकता है। यदि उस द्रव की वाष्पन की गुप्त ऊष्मा Hv ज्ञात हो ।

(iv) मोलल उन्नयन स्थिरांक और मोलर अवनमन स्थिरांक की गणना (Calculation of Molal Elevation Constnat and Molar Depression Constant):-

मोलल उन्नयन स्थिरांक (Molal Elevation Constant Kb):- जब एक मोल विलेय को 100 ग्राम विलायक में विलेय किया जाता है तो विलायक के क्वथनांक में हुआ उन्नयन मोलल उन्नयन स्थिरांक कहलाता है ।

माना कि w ग्राम विलेय जिसका अणुभार m है को 1000 ग्राम विलायक में विलेय किया जाता है तो माना कि क्वथनांक उन्नयन Tb होता है।

शुद्ध विलायक का क्वथनांक T तथा विलयन का क्वथनांक (T + Tb) पर वायुमण्डलीय दाब P है। यदि विलायक का वाष्प दाब (T + Tb) ताप पर P2 हो तो उसकी गणना क्लेसियस क्लेपीरॉन समीकरण द्वारा की जाती है।

चूंकि P2 – P1 का मान बहुत कम होता है इसलिये बची हुई संख्याओं को सूक्ष्म मान कर छोड़ा जा सकता है। है।

राऊल के नियम के अनुसार

समीकरण (58) से मोलल उन्नयन स्थिरांक Kb का मान ज्ञात किया जा सकता है।

(v) मोलल अवनमन स्थिरांक की गणना (Calculation of Molal Depression Constant):-

जिस प्रकार से मोलल उन्नयन स्थिरांक का व्यंजक व्युत्पन्न किया गया है, ठीक उसी प्रकार से मोलल अवनमन स्थिरांक का व्यंजक भी व्युत्पन्न किया जाता है, जो कि निम्न प्रकार है-