ब्रेवे जालक क्या है , ब्रेवे जालक के सभी प्रकार (bravais lattice in hindi) परिभाषा किसे कहते है

SbistudyDecember 21, 2018May 8, 2024inchemistry

(bravais lattice in hindi) ब्रेवे जालक क्या है परिभाषा किसे कहते है

परिभाषा : ब्रेवे फ़्रांस के गणितज्ञ थे जिन्होंने क्रिस्टल की संरचना पर अध्ययन किया और इसके आधार पर 1848 में निम्न बातें बताई –
एकक कोष्ठिका में अवयवी कणों की स्थिति के आधार पर सात प्रकार के क्रिस्टल तंत्र या समूह होते है।
एकक कोष्ठिका में अवयवी कण जैसे अणु , परमाणु या आयन की स्थिति के आधार पर इन 7 क्रिस्टल समुदायों को 14 प्रकार की त्रिविम जालकों में विभाजित किया जा सकता है और इन्ही 14 प्रकार के त्रिविम जालकों को ही ब्रेवे जालक कहते है।

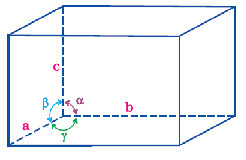
चित्र में एक एकक कोष्ठिका को प्रदर्शित किया गया है , माना चित्रानुसार किसी एकक कोष्ठिका के कोनो की लम्बाई क्रमश: a , b और c है। माना b और c सिरों के मध्य का कोण α है , सिरों a और c के मध्य का कोण β है तथा सिरों a और b के मध्य का कोण γ है।
फ़्रांस के गणितज्ञ ब्रेवे के अनुसार इन किनारों की लम्बाई a , b , और c तथा इनके मध्य बने कोणों α, β, γ के अलग अलग मान के आधार पर एकक कोष्ठिका की 14 आकृतियाँ संभव है अर्थात इनके भिन्न भिन्न मान के लिए 14 प्रकार के त्रिविम जालक संभव है , इन्ही 14 प्रकार के त्रिविम जालकों को ब्रेवे जालक कहा जाता है।
14 ब्रेवे जालक निम्न है –
1. घनीय (cubic) : इसमें तीनों सिरों की लम्बाई समान होती है तथा तीनो सिरे एक दुसरे के लम्बवत होते है अर्थात तीनों सिरों के मध्य का कोण 90 होता है –

a = b = c और α = β = γ = 90 डिग्री
2. अंत: केन्द्रित (body centred) :

इसमें भी तीनो भुजाएं समान लम्बाई की होती है और तीनो एक दुसरे के लम्बवत स्थित होती है .
a = b = c और α = β = γ = 90 डिग्री

3. फलक केन्द्रित (face centred)

इस प्रकार के त्रिविम जालक में तीनो भुजाओं की लम्बाई बराबर होती है और सभी एक दूसरे के लम्बवत स्थित रहती है अर्थात इन भुजाओं के मध्य कोण का मान 90 डिग्री होता है।

a = b = c और α = β = γ = 90 डिग्री

4. द्विसमलम्बाक्ष (tetragonal) (आद्य)

दो अक्षों की लम्बाई समान होती है और तीसरे अक्ष की लम्बाई भिन्न होती है तथा तीनो एक दुसरे के लम्बवत होते है –

a = b ≠ c and α = β = γ = 90 डिग्री

5. द्विसमलम्बाक्ष (tetragonal) (अंत: केन्द्रित)

इसमें भी a = b ≠ c and α = β = γ = 90 डिग्री

6. विषम लम्बाक्ष (Orthorhombic) (आद्य)

इसमें तीनों भुजाओं की लम्बाई ही एक दुसरे से भिन्न होती है लेकिन तीनों भुजाएं एक दुसरे के लम्बवत होते है अर्थात सभी भुजाओं के मध्य का कोण 90 डिग्री होता है –

a ≠ b ≠ c and α = β = γ = 90 डिग्री

7. विषम लम्बाक्ष (Orthorhombic) (अंत: केन्द्रित)

इसमें भी a ≠ b ≠ c and α = β = γ = 90 डिग्री

8. विषम लम्बाक्ष (Orthorhombic) (फलक केन्द्रित)

इसमें भी सभी अक्षीय लम्बाई असमान और एक दुसरे के लम्बवत अर्थात a ≠ b ≠ c and α = β = γ = 90 डिग्री

9. विषम लम्बाक्ष (Orthorhombic) (अन्त्य केंद्रित)

इसमें भी निम्न सम्बन्ध होगा – a ≠ b ≠ c and α = β = γ = 90 डिग्री

10. एकनताक्ष (Monoclinic) (आद्य)

इसमें तीनो अक्षीय भुजाओं की लम्बाई अलग अलग होती है , दो अक्षीय कोण 90 डिग्री के होते है लेकिन एक अक्षीय कोण का मान 90 डिग्री नही होता है।

a ≠ b ≠ c तथा α = β = 90 , γ ≠ 90 डिग्री

11. एकनताक्ष (Monoclinic) (अन्त्य केन्द्रित)

इसमें भी निम्न सम्बन्ध होता है – a ≠ b ≠ c तथा α = β = 90 , γ ≠ 90 डिग्री

12. षट्कोणीय (Hexagonal)

दो अक्षीय भुजा समान लम्बाई की होती है और एक भुजा की लम्बाई भिन्न होती है तथा दो अक्षीय कोण 90 डिग्री और एक अक्षीय कोण का मान 120 डिग्री होता है।

a = b ≠ c तथा α = β = 90 ∘ , γ = 120
13. त्रिसमनताक्ष (rhombohedral) (trigonal) (आद्य)
इसमें तीनो भुजाओं की अक्षीय लम्बाई समान होती है के होते है तथा तीनो कोण भी समान होते है लेकिन तीनो कोण का मान 90 डिग्री नही होता है

a = b = c तथा α=β=γ ≠90
14. त्रिनताक्ष (Triclinic)
इसमें तीनो अक्षीय लम्बाई और अक्षीय कोण असमान होते है .

a ≠ b ≠ c और α ≠ β ≠ γ

ब्रेवे जालक (bravais lattice in hindi) : फ्रांस के गणितज्ञ ब्रेवे ने 1848 में बताया कि सात क्रिस्टल समुदायों को उनकी एकक कोष्ठिका में अवयवी कणों की व्यवस्था के आधार पर 14 विभिन्न प्रकार के त्रिविम जालकों में विभाजित किया जा सकता है। इन त्रिविम जालकों को ब्रेवे जालक कहते है।

ब्रेवे जालकों को सारणी में व्यवस्थित किया गया है। सारणी में दर्शाया गया है। कि एक क्रिस्टल समुदाय में कौन कौन से एकक कोष्ठिकाएँ संभव है तथा उनकी कुल संख्या कितनी है।

क्रिस्टल समुदाय	त्रिविम जालकों (एक कोष्ठिकाओं) के प्रकार	त्रिविम जालकों की संख्या
1. घनीय	आद्य , अंत: केन्द्रित फलक केन्द्रित	3
2. द्विसमलम्बाक्ष चतुष्कोणीय	आद्य , अंत: केन्द्रित	2
3. विषमलम्बाक्ष	आद्य , अंत: केन्द्रित अन्त्य केन्द्रित , फलक केन्द्रित	4
4. एकनताक्ष	आद्य , अंत्य केन्द्रित	2
5. षट्कोणीय	आद्य	1
6. त्रिसमनताक्ष (अथवा त्रिकोणी)	आद्य	1
7. त्रिनताक्ष	आद्य	1