यदि X = {1, 2, 3, 4}तथा Y = {a, b, c} तो कारण सहित सिद्ध कीजिए कि यह बहु-एक आच्छादक प्रतिचित्रण है। (चित्र देखे)
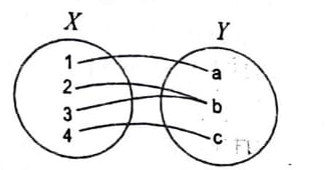
उदाहरण 8. यदि X = {1, 2, 3, 4}तथा Y = {a, b, c} तो कारण सहित सिद्ध कीजिए कि यह बहु-एक आच्छादक प्रतिचित्रण है। (चित्र देखे)
हल : चित्रानुसार X के दो अवयव 2 तथा 3 ऐसे हैं । जिनका प्रतिबिम्ब Y में है है, इसलिए यह बहु-एक फलन है । स्पष्टत: Y का प्रत्येक अवयव X के कम-से-कम एक अवयव का प्रतिबिम्ब है, अतः फलन आच्छादक है।
अतः दिया हुआ फलन बहु-एक आच्छादक है।
उदाहरण 9. यदि X सभी त्रिभुजों का समुच्चय है और y वास्तविक धन संख्याओं का समुच्चय है, तो सिद्ध कीजिए कि फलन f: X → Y, जहाँ f (4) त्रिभुजों का क्षेत्रफल (E X) बहु- एक आच्छादक है।
हल : चूँकि त्रिभुज का क्षेत्रफल धनात्मक वास्तविक संख्या है तथा दो अथवा दो से अधिक त्रिभुजों के क्षेत्रफल समान हो सकते हैं।
डोमेन X के दो या दो से अधिक अवयवों का सहडोमेन Y में एक ही f- प्रतिविम्ब होगा।
f बहु-एक (many-one) फलन है।
पुनः सहडोमेन Y की प्रत्येक वास्तविक धन संख्या, डोमेन X के किसी त्रिभुज के क्षेत्रफल के बराबर अवश्य होगी।
सहडोमेन Y का प्रत्येक अवयव, डोमेन X के किसी अवयव का – प्रतिबिम्ब है।
आच्छादक ( onto ) है।
अत:, बहु-एक आच्छादक (many-one onto ) है ।
उदाहरण 10. यदि वास्तविक संख्याओं के समुच्चय R पर फलन f: R → R इस प्रकार परिभाषित है कि f(x) = ext, x e R, तो सिद्ध कीजिए कि एकैकी है।
हल माना डोमेन R के कोई दो अवयव x1 तथा x2 हैं :
अर्थात् ×1, ×2 ∈ R, तब
दिया गया फलन एकैकी (one-one) है।
उदाहरण 11. यदि A = {a, b, c} तथा B = {x, y, z} तो दिखाइए कि निम्नलिखित समुच्चय A से समुच्चय B में फलन है या नहीं :
हल: (i) यह फलन नहीं है क्योंकि CEA का कोई भी प्रतिबिम्ब B में नहीं है अर्थात् 1 के अवयव के संगत B में कोई अवयव नहीं है।
(ii) यह फलन है क्योंकि समुच्चय 4 के प्रत्येक अवयव के संगत समुच्चय B में एक अवयव है।
(iii) यह फलन बहु-एक अन्त:क्षेपी है, क्योंकि B का ■ अवयव समुच्चय 4 के किसी अवयव का प्रतिबिम्ब नहीं है।
(iv) यह फलन बहु-एक आच्छादक है, क्योंकि B का प्रत्येक अवयव समुच्चय 4 के अवयवों का प्रतिबिम्ब है तथा C E A के दो प्रतिबिम्ब समुच्चय B में हैं जो कि x तथा z हैं।
उदाहरण 12. यदि A = {1, 2, 3} तथा B = {x, y} तो A से B पर कितने प्रकार के फलन बनाए जा सकते हैं ? हल: A से B पर निम्न फलन बनाए जा सकते हैं :
(i) 1 → x 2 x 3 → x (बहुएक अन्त:क्षेपी)
(ii) 1→ x, 2 → x 3 → y ( बहुएक आच्छादक)
(iii) 1→ x, 2 →)y, 3→ y (बहुएक आच्छादक)
(iv) 1 → x, 2 → y 3 →x ( बहुएक आच्छादक)
(v) 1 →y, 2 → x 3 → y (बहुएक आच्छादक)
(vi) 1, 2 ⇒ x 3 → x (बहुएक आच्छादक)
(vii) 1 → y, 2 → y, 3→ x (बहुएक आच्छादक)
(viii) 1→y, 2 → y. 3→y ( बहुएक अन्त:क्षेपी)
(विद्यार्थी इन्हें चित्र बनाकर देख सकते हैं। )
[ टिप्पणी: यदि 4 तथा B दो समुच्चय हैं जिनमें क्रमश: m तथा अवयव हों तो समुच्चय A से समुच्चय B पर कुल फलनों की संख्या ” होगी।
n (A) = 3, n (B) = 2,
फलनों की संख्या 23 = 8]
उदाहरण 13. यदि f: A → A निम्न प्रकार परिभाषित है (0) (x) – ‘, (ii) f (x) = sin x जहाँ A = {-1, 1}, तो क्या यह आच्छादक है?
हल : (i) f (x) = x 3 आच्छादक है, क्योंकि
f (1) = 13 = 1 ∈ A, f (- 1) = (- 1)3 ∈ A = -1 ∈ A अर्थात् डोमेन A के प्रत्येक अवयव के संगत सहडोमेन A में एक अवयव है।
(ii) f(x) = sin.x, आच्छादक नहीं है क्योंकि 4 में कोई अवयव ऐसा नहीं है जिसके लिए sin x = 1.
उदाहरण 14. किस प्रतिबन्ध के अन्तर्गत अचर फलन आच्छादक होता है।
हल: यदि फलन के परिसर (Range) में केवल एक ही अवयव हो तो फलन हमेशा अचर तथा आच्छादक होता है।
उदाहरण 15. यदि A = {x x e R x ≠ 0} तो सिद्ध कीजिए कि फलन : A – A जो कि इस प्रकार परिभाषित है :होगा ।
F (x) = 1/x एकैकी आच्छादक (one-one onto)
हल : स्पष्टत: परिसर (Range) का प्रत्येक अवयव डोमेन का एक अवयव है, क्योंकि
f (x) = 1/x
तब f(1) = 1/1 = 1, जो वास्तविक संख्या है।
अतः f (2) = 2. जो वास्तविक संख्या है।
अतः फलन आच्छादक है।
पुनः परिसर का कोई भी अवयव डोमेन के एक से अधिक अवयव का प्रतिबिम्ब नहीं है अर्थात् डोमेन के प्रत्येक अवयव के लिए परिसर में एक और केवल एक प्रतिबिम्ब है जैसे कि 5 का प्रतिबिम्ब 1/5 होगा, (अर्थात् f(5) = 1/5 )
अतः फलन एकैकी है।
उदाहरण 16. यदि Z पूर्णांकों का समुच्चय हो तथा इस पर फलन ∫ : Z→ Z है, तो निम्नलिखित फलनों की
जाँच कीजिए:
(i) f (x) = x5
(ii) f (x) = x +3
(iii) f (x) = 3x + 4.
हल : (i) f (x) = x, यदि x1 x2 कोई दो पूर्णांक z में हैं। अर्थात् x1, x2 EZ,
अतएव फलन का
डोमेन = {….- 4-3 – 2 – 1, 0, 1, 2, 3…}
परिसर = {…..- 1024243, 32, 10, 1, 32, 243, 1024,….}
अर्थात् परिसर (Range) cz
फलन, अन्तःक्षेपी है।
अतः दिया हुआ फलन एकैकी अन्तः क्षेपी है।
(ii) f (x) x + 3
यदि x 1 x 2 E Z, तो
f (xi) = f (x2) ⇒ x1 + 3 = x2 + 3
=> X1 = x2
अतः फलन एकैकी है।
माना सहडोमेन का कोई स्वेच्छ अवयव y है।
यदि f (x) = y, तो
y = x + 3 = x =(y-3) Ez (डोमेन)
.. f (y – 3 ) = (y – 3) + 3
= y
अतः फलन आच्छादक है।
. दिया हुआ फलन एकैकी आच्छादक है।
(iii) f(x) = 3x + 4,
यदि X1, X2 E ,Z तो
f (x 1) = f (x2) = 3×1 + 4 = 3×2 + 4
=> 3×1 = 3×2
=> X1 X2
अतः फलन एकैकी है।
f (x) = 3x + 4
f(1) = 3·1 + 4 = 7
f(2) = 3-2 + 4 = 10
f(3) = 3-3 + 4 =13
f (-1) = 3 (-1) + 4 = 1
f(-2) = 3 (-2) + 4 =- 2
( 2 ) = (…. – 2, 1, 7, 10, 13…. } c Z
फलन अन्तःक्षेपी है।
अतः दिया हुआ फलन एकैकी तथा अन्तःक्षेपी है।
उदाहरण 17. सिद्ध कीजिए कि फलन f : R – R f(x) = | x | न तो एकैकी है और न ही आच्छादक। [यहाँ f(x) = | x |, मापांक फलन (Modulus function) है । ]
हल: f(x) = | x |
अब (1) = | 1 | = 1 तथा (- 1) = | – 1 | = 1 स्पष्टत: डोमेन के दो अवयवों तथा 1 का प्रतिबिम्ब एक ही अवयव 1 है।
F एकैकी नहीं है।
पुनः प्रत्येक वास्तविक संख्या धनात्मक या ऋणात्मक के लिए | x | हमेशा धनात्मक होगी तथा x = 0, | x | = 0 होगा। हम देखते हैं कि सहडोमेन के सभी अवयव 0 अथवा धनात्मक हैं अर्थात्
सहडोमेन = {x : x > 0, X E R} R
या f (R) R
फलन आच्छादक नहीं है।
अतः फलन न तो एकैकी है और न ही आच्छादक ।
उदाहरण 18. सिद्ध कीजिए कि फलन f: RR : f(x) = [x] न तो एकैकी है और न ही आच्छादक (/(x) = [x]; महत्तम पूर्णांक फलन (greatest integer func tion) है ।।
हल : वास्तविक संख्याओं 1.5 तथा 1-7 के लिए
स्पष्टतः दो वास्तविक संख्याओं 1.5 तथा 1-7 का प्रतिबिम्ब एक ही वास्तविक संख्या 1 है।
फलन एकैकी नहीं है।
पुनः कोई ऐसी वास्तविक संख्या x ऐसी नहीं है जिसके लिए f(x) = [x] = 1.4
अर्थात् सहडोमेन में सभी अवयव पूर्णांक होंगे,
अर्थात् f(x) R
फलन / आच्छादक नहीं है।
उदाहरण 19. यदि 4 = R {4} तथा B = R – {1} तथा फलन f: AB इस प्रकार परिभाषित है कि
सिद्ध कीजिए कि f एकैकी आच्छादक है।
हल: यदि x1, x2 E A, तब
फलन एकैकी है।”
माना y e B इस प्रकार है कि y = f(x)
स्पष्टत: y = 1 के लिए x परिभाषित है ।
x=4
फलन F आच्छादक है।
अतः दिया हुआ फलन एकैकी आच्छादक है।
उदाहरण 20. सिद्ध कीजिए कि चिह्न फलन f = R – R, जो निम्न प्रकार परिभाषित है :
न तो एकैकी है और न आच्छादक है।
अर्थात् दो वास्तविक संख्याओं 3/2 तथा 5/2 का एक ही वास्तविक प्रतिबिम्ब 1 है।
फलन f एकैकी नहीं है।
पुनः हम देखते हैं कि फलन का सहडोमेन प्रत्येक वास्तविक संख्या के लिए – 1, 0, 1} है।
अतः सहडोमेन – 1, 0, 1)} R
या परिसर ( Range) = {-1, 0, 1}
फलन अन्त:क्षेपी है।
अतः चिह्न फलन न तो एकैकी है और न ही आच्छादक :
उदाहरण 21. सिद्ध कीजिए कि फलन
जो इस प्रकार परिभाषित है कि
एकैकी तथा आच्छादक है।
F आच्छादक है।
[ डोमेन [0, 00) तथा सहडोमेन (0, 2)]
अतः फलन एकैकी तथा आच्छादक है।
(ii) जव x < 0, तब
f(x) = x /x 2
माना, y e ( -2, 0) एक स्वेच्छ वास्तविक संख्या इस प्रकार है कि f (x)=y तब
F आच्छादक है।
[ यहाँ डोमेन ( – 00, 0) तथा परिसर ( – 2, 0) .. फलन एकैकी तथा आच्छादक है ।]
अतः इस प्रकार हम कह सकते हैं कि फलन f: R – {x e R:- 2 < x < 2} एकैकी तथा आच्छादक है।
उदाहरण 22. यदि A तथा B दो समुच्चय हैं तथा फलन f: A × B ⇒ B × A इस प्रकार परिभाषित है कि f(a, b) = (b, a) तो सिद्ध कीजिए कि फलन एकैकी आच्छादक है।
हल: यदि (a1, b1) तथा (a2, b2) ∈ Ax B तब
F (a1, b1) = f(a2, b2) (b1, a1 ) = (b2. a2)
= → b1 = b2 = a1 = a2
→ (a1, b1) = (a2, b2)
फलन एकैकी है।
पुनः माना ( b, a), B x 4 का एक स्वेच्छ अवयव है। तथा b e B तथा a E A
.
f : A × B → B × 4 आच्छादक है।
अतः दिया गया फलन एकैकी आच्छादक है।
उदाहरण 23. यदि ∫ : N x N निम्न प्रकार परिभाषित
तो सिद्ध कीजिए कि फलन : f : N x N बहु-एकैकी आच्छादक है।
अतः 1 = 2 = (1) = f(2)
f बहु-एकैकी है।
पुनः यदि समुच्चय N का कोई स्वेच्छ अवयव n हो तथा n विषम है तो (2n – 1) भी विषम होगा ।
अतः दिए गए फलन की परिभाषानुसार,
जो प्राकृत संख्या है।
यदि n सम हो तो 2n भी सम होगा तब
जो प्राकृत संख्या है।
इस प्रकार हम देखते हैं कि n e N (n सम हो अथवा विषम)
f(n) = N.
फलन आच्छादक है।
अतः दिया गया फलन बहु- एकैकी आच्छादक है।
उदाहरण 24. यदि फलन : AB के डोमेन 4 पर सम्बन्ध R इस प्रकार परिभाषित है कि :
R = {(a, b) ; f (a) = f(b)}
तो सिद्ध कीजिए कि सम्बन्ध R तुल्यता सम्बन्ध है ।
हल: फलन f : A → B
तथा सम्बन्ध R = (a, b): f (a) = f (b)}
(i) सम्बन्ध R स्वतुल्य है, क्योंकि यदि a E X तब
f(a) = f(a) = (a, a) ∈ R अर्थात् aRa.
(ii) R सममित है क्योंकि यदि (a, b) E R, तब
(a, b) E R f (a) = f (b)
= f (b) = f (a)
(b, a) e R
(iii) R संक्रमक है,
माना (a, b) E R तथा (b, c) E R तब,
(a, b) ∈ R, (b, c) E R
⇒ f(a) = f(b) तथा (b) = f(c)
= f(a) = f (b) = f (c)
=> f (a) = f (c)
(a, c) e R
(a, b) e R, (b, c) e R (a, c) e R
चूँकि सम्बन्ध R, समुच्चय X पर स्वतुल्य, सममित तथा संक्रमक है। अतः यह तुल्यता सम्बन्ध है।
हिंदी माध्यम नोट्स
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi sociology physics physical education maths english economics geography History
chemistry business studies biology accountancy political science
Class 12
Hindi physics physical education maths english economics
chemistry business studies biology accountancy Political science History sociology
English medium Notes
Class 6
Hindi social science science maths English
Class 7
Hindi social science science maths English
Class 8
Hindi social science science maths English
Class 9
Hindi social science science Maths English
Class 10
Hindi Social science science Maths English
Class 11
Hindi physics physical education maths entrepreneurship english economics
chemistry business studies biology accountancy
Class 12
Hindi physics physical education maths entrepreneurship english economics